2023-2024學年四川省南充市閬中中學高三（上）月考數學試卷（理科）（10月份）

一、選擇題：本題共12小題，每小題5分，共60分．在每小題給出的四個選項中，只有一項是符合題目要求的．

• 1．設集合M={y|y=2cosx,x∈[0，5]}，N={x|y=log₂（x-1）}，則M∩N=（　　）

  A．{x|1＜x≤5}

  B．{x|-1＜x≤0}

  C．{x|-2≤x≤0}

  D．{x|1＜x≤2}
  組卷：33引用：2難度：0.7

  解析

• 2．已知a,b∈R，（a-i）i=b-2i,則a+bi的共軛復數為（　　）

  A．-2-i

  B．-2+i

  C．2-i

  D．2+i
  組卷：133引用：7難度：0.8

  解析

• 3．方程x²+2ax-a=0在區間（0，1）和（1，2）各有一個根的充要條件是（　　）

  A．a∈（-∞，-1）

  B． a ∈ （ - 4 3 ，- 1 ）

  C． a ∈ （ - 4 3 ， 0 ）

  D．a∈（-2，-1）
  組卷：316引用：6難度：0.5

  解析

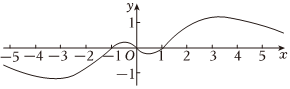• 4．已知函數f（x）的部分圖象如圖所示，則f（x）的解析式可能為（　　）

  A．f（x）=x3?ln|x|	B．f（x）=e|x|?（x2-1）
  C． f （ x ） = x 3 - x e | x |	D． f （ x ） = x - x 3 2 x
  組卷：45引用：4難度：0.7

  解析

• 5．在數列{a_n}中，a₁=1，a_n+1=2a_n，S_n為等比數列{a_n}的前n項和，若{S_n+λ}為等比數列，則λ=（　　）

  A．-1

  B．1

  C．-2

  D．2
  組卷：96引用：2難度：0.7

  解析

• 6．已知向量

  m

  =

  （

  2

  3

  ，

  cosθ

  ）

  ，

  n

  =

  （

  sinθ

  ，

  2

  ）

  ，

  m

  ?

  n

  =

  1

  ，則

  cos

  （

  2

  θ

  -

  2

  π

  3

  ）

  的值是（　　）

  A． 7 8

  B． 1 4

  C． - 1 4

  D． - 7 8
  組卷：103引用：4難度：0.5

  解析

• 7．8月29日，華為在官方網站發布了Mate60手機，其中大部分件已實現國產化，5G技術更是遙遙領先，5G技術的數學原理之一便是著名的香農公式：

  C

  =

  W

  lo

  g

  2

  （

  1

  +

  S

  N

  ）

  ，它表示：在受噪聲干擾的信道中，最大信息傳遞速度C取決于信道帶寬W，位道內信號的平均功率S以及信道內部的高斯噪聲功率N的大小，其中

  S

  N

  叫做信噪比．當信噪比比較大時，公式中真數中的1可以忽略不計．按照香農公式，若不改變帶寬W，而將信噪比從1000提升至5000，則C大約增加了（　　）（參考數值：lg2≈0.301）

  A．43%

  B．33%

  C．23%

  D．13%
  組卷：210引用：11難度：0.7

  解析

（二）選考題：共10分．請考生在第22、23題中任選一題作答，如果多做，則按所做的第一題計分．[選修4-4：坐標系與參數方程]?

• 22．在直角坐標系xOy中，曲線C₁的參數方程為

  x = 2 2 t

  y = t 2 - 1

  （t為參數）．以坐標原點為極點，x軸正半軸為極軸建立極坐標系，曲線C₂的極坐標方程為ρcosθ+ρsinθ-1=0．
  （1）求C₁的普通方程與C₂的直角坐標方程；
  （2）設M，N是C₁與C₂的公共點，點P的直角坐標為（0，1），求

  1

  |

  PM

  |

  +

  1

  |

  PN

  |

  的值．
  組卷：142引用：3難度：0.6

  解析

[選修4-5：不等式選講]?

• 23．已知a,b,c是正實數，且滿足

  a

  +

  b

  2

  +

  c

  3

  =

  1

  ．
  （1）是否存在滿足已知條件的a,b,使得ab=

  1

  2

  ，試說明理由；
  （2）求

  a

  +

  b

  +

  c

  的最大值．
  組卷：209引用：4難度：0.7

  解析