2022-2023學年四川省成都市樹德中學光華校區高一（下）期末數學模擬試卷（3）

一、單選題（共40分）

• 1．已知復數z滿足

  z

  1

  +

  2

  i

  =

  2

  -

  i

  ，則

  z

  =（　　）

  A．4-3i

  B．4+3i

  C．3-4i

  D．3+4i
  組卷：51引用：4難度：0.8

  解析

• 2．已知m,n是兩條不同的直線，α，β是兩個不同的平面，則（　　）

  A．若m∥α，n∥α，則m∥n	B．若m∥α，m⊥n,則n⊥α
  C．若α∥β，m⊥α，n∥β，則m⊥n	D．若m∥n,n?α，則m∥α
  組卷：938引用：10難度：0.7

  解析

• 3．若向量

  a

  =

  （

  1

  ，

  0

  ）

  ，

  b

  =

  （

  2

  ，

  1

  ）

  ，則向量

  a

  在向量

  b

  上的投影向量為（　　）

  A． 2 5 5

  B． （ 4 5 ， 2 5 ）

  C． （ 4 5 5 ， 2 5 5 ）

  D．（4，2）
  組卷：98引用：1難度：0.8

  解析

• 4．已知一個直三棱柱的高為1，如圖，其底面△ABC水平放置的直觀圖（斜二測畫法）為△A′B′C′，其中O′A′=O′B′=O′C′=1，則該三棱柱的表面積為（　　）

  A． 6 + 2 2

  B． 6 + 4 2

  C． 6 + 2 5

  D． 6 + 4 5
  組卷：188引用：6難度：0.7

  解析

• 5．在《九章算術》中，將四個面都是直角三角形的四面體稱為鱉臑．在鱉臑A-BCD中AB⊥平面BCD，BC⊥CD，且AB=BC=CD=2，則鱉臑A-BCD外接球的表面積為（　　）

  A． 19 3 π

  B．6π

  C．12π

  D．16π
  組卷：327引用：4難度：0.6

  解析

• 6．已知

  α

  ∈

  （

  π

  ，

  3

  π

  2

  ）

  ，若

  1

  +

  sin

  2

  α

  1

  +

  cos

  2

  α

  =

  9

  2

  ，則tan2α的值是（　　）

  A． - 3 4

  B． 3 4

  C． - 4 3

  D． 4 3
  組卷：340引用：3難度：0.7

  解析

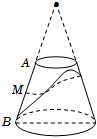• 7．一圓臺上底半徑為5cm,下底半徑為10cm,母線AB長為20cm,其中A在上底面上，B在下底面上，從AB中點M，拉一條繩子，繞圓臺的側面一周轉到B點，則這條繩子最短長為（　　）

  A．30cm

  B．40cm

  C．50cm

  D．60cm
  組卷：286引用：5難度：0.7

  解析

四、解答題（共70分）

• 21．在△ABC中，a,b,c分別為角A，B，C的對邊，平面內點O滿足（

  OA

  +

  OB

  ）?

  AB

  =（

  OB

  +

  OC

  ）?

  BC

  =（

  OC

  +

  OA

  ）?

  CA

  =0，且b²-2b+c²=0
  （1）證明：點O為△ABC的外心；
  （2）求

  BC

  ?

  AO

  的取值范圍．
  組卷：109引用：4難度：0.5

  解析

• 22．如圖，在四棱錐P-ABCD中，PB=PD，PA⊥PC，M，N分別為PA，BC的中點底面四邊形ABCD是邊長為2的菱形，且∠DAB=60°，AC交BD于點O．
  （1）求證：MN∥平面PCD；
  （2）二面角B-PC-D的平面角為θ，若

  cosθ

  =

  -

  1

  7

  ．
  ①求PA與底面ABCD所成角的大小；
  ②求點N到平面CDP的距離．
  組卷：256引用：3難度：0.6

  解析