當前位置：試卷中心 > 試卷詳情

2022-2023學年遼寧省沈陽市和平區東北育才學校高一（上）第二次段考數學試卷

發布：2024/11/19 9:30:2

一、單選題（共40分，每題5分.每題四個選項中有且只有一項是正確答案.）

1．集合
M
=
{
y
|
y
=
8
x
+
3
，
x
,
y
∈
Z
}
的元素個數是（　　）
A．2個 B．4個 C．6個 D．8個
組卷：89引用：3難度：0.8
解析
2．已知函數f（x）=a^x+b（a＞0，a≠1）的定義域和值域都是[-1，0]，則a+b=（　　）
A．
-
3
2
B．-1 C．1 D．
3
2
組卷：179引用：1難度：0.5
解析
3．函數f（x）=
sinx
+
x
cosx
+
x
2
在[-π，π]的圖象大致為（　　）
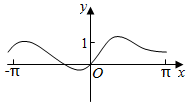
A． B．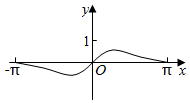
C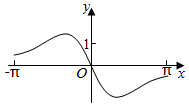． D．
組卷：9627引用：52難度：0.8
解析
4．已知直線
x
=
π
3
和
x
=
2
π
3
是曲線f（x）=2sin（ωx+φ）（-π＜φ≤π）的兩條對稱軸，且函數f（x）在
（
π
2
，

2
π
3
）
上單調遞減，則φ的值是（　　）
A．
-
π
2
B．0 C．
π
2
D．π
組卷：292引用：5難度：0.7
解析
5．若正數a,b滿足4a+3b-1=0，則
1
2
a
+
b
+
1
a
+
b
的最小值為（　　）
A．
3
+
2
2
B．
1
+
2
2
C．2
+
3
2
D．
2
2
組卷：1148引用：6難度：0.6
解析
6．如圖，在△ABC中，
BD
=3
DC
，
AE
=m
AB
，
AF
=n
AC
，m＞0，n＞0，則
1
m
+
3
n
=（　　）
A．3 B．4 C．
4
3
D．
3
4
組卷：1459引用：3難度：0.5
解析
7．已知函數f（x）=sinx,函數g（x）的圖象可以由函數f（x）的圖象先向右平移
π
6
個單位長度，再將所得函數圖象保持縱坐標不變，橫坐標變為原來的
1
ω
（
ω
＞
0
）
得到．若函數g（x）在（0，π）上恰有5個零點，則ω的取值范圍是（　　）
A．
[
31
6
，
37
6
）
B．
（
31
6
，
37
6
]
C．
[
25
6
，
31
6
）
D．
（
25
6
，
31
6
]
組卷：192引用：4難度：0.6
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題（本大題共6小題，共72.0分.解答應寫出文字說明，證明過程或演算步驟）

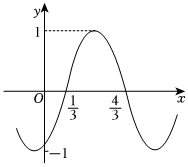21．已知函數
f
（
x
）
=
A
sin
（
ωx
+
φ
）
（
A
＞
0
，
ω
＞
0
，
|
φ
|
＜
π
2
）
的部分圖象如圖所示．
（1）求A，ω和φ的值；
（2）求函數y=f（x）在[1，2]上的單調遞減區間；
（3）若函數y=f（x）在區間[a,b]上恰有2022個零點，求b-a的取值范圍．
組卷：473引用：2難度：0.5
解析
22．設定義在R上的函數f（x）滿足：①對?x,y∈R，都有
f
（
x
+
y
）
=
f
（
x
）
+
f
（
y
）
1
+
f
（
x
）
f
（
y
）
；②x＞0時，f（x）＞0；③不存在x∈R，使得|f（x）|=1．
（1）求證：f（x）為奇函數；
（2）求證：f（x）在R上單調遞增；
（3）設函數g（x）=x²-x-3，
f
（
1
）
=
1
2
，不等式
4
+
5
f
（
mx
）
5
+
4
f
（
mx
）
＞
1
+
2
f
（
m
x
2
）
2
+
f
（
m
x
2
）
對?x∈R恒成立，試求g（m）的值域．
組卷：626引用：4難度：0.3
解析

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

A．	B．
C．	D．

2022-2023學年遼寧省沈陽市和平區東北育才學校高一（上）第二次段考數學試卷

一、單選題（共40分，每題5分.每題四個選項中有且只有一項是正確答案.）

1．集合M={y|y=8x+3，x,y∈Z}的元素個數是（ ）

2．已知函數f（x）=ax+b（a＞0，a≠1）的定義域和值域都是[-1，0]，則a+b=（ ）

3．函數f（x）=sinx+xcosx+x2在[-π，π]的圖象大致為（ ）

4．已知直線x=π3和x=2π3是曲線f（x）=2sin（ωx+φ）（-π＜φ≤π）的兩條對稱軸，且函數f（x）在（π2， 2π3）上單調遞減，則φ的值是（ ）

5．若正數a,b滿足4a+3b-1=0，則12a+b+1a+b的最小值為（ ）

6．如圖，在△ABC中，BD=3DC，AE=mAB，AF=nAC，m＞0，n＞0，則1m+3n=（ ）

四、解答題（本大題共6小題，共72.0分.解答應寫出文字說明，證明過程或演算步驟）

21．已知函數f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜π2）的部分圖象如圖所示．（1）求A，ω和φ的值；（2）求函數y=f（x）在[1，2]上的單調遞減區間；（3）若函數y=f（x）在區間[a,b]上恰有2022個零點，求b-a的取值范圍．

1．集合
M
=
{
y
|
y
=
8
x
+
3
，
x
,
y
∈
Z
}
的元素個數是（　　）

2．已知函數f（x）=a^x+b（a＞0，a≠1）的定義域和值域都是[-1，0]，則a+b=（　　）

3．函數f（x）=
sinx
+
x
cosx
+
x
2
在[-π，π]的圖象大致為（　　）

4．已知直線
x
=
π
3
和
x
=
2
π
3
是曲線f（x）=2sin（ωx+φ）（-π＜φ≤π）的兩條對稱軸，且函數f（x）在
（
π
2
，

2
π
3
）
上單調遞減，則φ的值是（　　）

5．若正數a,b滿足4a+3b-1=0，則
1
2
a
+
b
+
1
a
+
b
的最小值為（　　）

6．如圖，在△ABC中，
BD
=3
DC
，
AE
=m
AB
，
AF
=n
AC
，m＞0，n＞0，則
1
m
+
3
n
=（　　）