2022-2023學(xué)年吉林省長(zhǎng)春十一中高二(下)期末數(shù)學(xué)試卷
發(fā)布:2024/6/25 8:0:9
一、選擇題:本題共8小題,每小題5分,在每小題給出的四個(gè)選項(xiàng)中,只有一個(gè)選項(xiàng)是符合題目要求的.
-
1.已知全集U=R,設(shè)集合A={x|x-1<0},B={x|x2-2x-3≤0},則(?UA)∪B=( )
A.{x|1≤x≤3} B.{x|-2≤x<1} C.{x|x≥-1} D.{x|x≤3} 組卷:202引用:4難度:0.7 -
2.某物體做直線運(yùn)動(dòng),其運(yùn)動(dòng)規(guī)律是
,則它在第4秒末的瞬時(shí)速度為( )s=t2+3tA. 米/秒12316B. 米/秒12516C.8米/秒 D. 米/秒674組卷:79引用:4難度:0.9 -
3.已知函數(shù)
,則f(x)的零點(diǎn)所在的區(qū)間為( )f(x)=lnx+x-2xA.(-1,1) B.(1,2) C.(2,e) D.(e,3) 組卷:220引用:6難度:0.8 -
4.隨著疫情結(jié)束,自行車市場(chǎng)逐漸回暖,通過(guò)調(diào)查,收集了5家商家對(duì)某個(gè)品牌的自行車的售價(jià)x(百元)和月銷售量y(百輛)之間的一組數(shù)據(jù),如表所示:
根據(jù)計(jì)算可得y與x的經(jīng)驗(yàn)回歸方程是:價(jià)格x 9.6 9.9 10 10.2 10.3 銷售y 10.2 9.3 m 8.4 8.0 ,則m的值為( )?y=-3.1x+40A.8.8 B.8.9 C.9 D.9.1 組卷:52引用:5難度:0.6 -
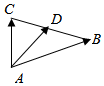 5.已知||=2a,|2|=3,b,a的夾角為b,如圖所示,若π4=5AB+2a,b=AC-3a,且D為BC中點(diǎn),則b的長(zhǎng)度為( )AD
5.已知||=2a,|2|=3,b,a的夾角為b,如圖所示,若π4=5AB+2a,b=AC-3a,且D為BC中點(diǎn),則b的長(zhǎng)度為( )ADA. 152B. 152C.7 D.8 組卷:1371引用:8難度:0.9 -
6.我們將服從二項(xiàng)分布的隨機(jī)變量稱為二項(xiàng)隨機(jī)變量,服從正態(tài)分布的隨機(jī)變量稱為正態(tài)隨機(jī)變量.概率論中有一個(gè)重要的結(jié)論是棣莫弗一拉普拉斯極限定理,它表明,若隨機(jī)變量Y~B(n,p),當(dāng)n充分大時(shí),二項(xiàng)隨機(jī)變量Y可以由正態(tài)隨機(jī)變量X來(lái)近似,且正態(tài)隨機(jī)變量X的期望和方差與二項(xiàng)隨機(jī)變量Y的期望和方差相同.棣莫弗在1733年證明了
的特殊情形,1812年,拉普拉斯對(duì)一般的p進(jìn)行了證明.現(xiàn)拋擲一枚質(zhì)地均勻的硬幣100次,則利用正態(tài)分布近似估算硬幣正面向上次數(shù)超過(guò)60次的概率為( )p=12
(附:若X~N(μ,σ2),則P(μ-σ≤X≤μ+σ)≈0.6827,P(μ-2σ≤X≤μ+2σ)≈0.9545,P(μ-3σ≤X≤μ+3σ)≈0.9973)A.0.1587 B.0.0228 C.0.0027 D.0.0014 組卷:364引用:10難度:0.8 -
7.已知定義在R上的函數(shù)f(x)滿足f(x)+f(-x)=0,f(-x-1)=f(-x+1),當(dāng)x∈(0,1)時(shí),f(x)=4x-3,則f(log480)=( )
A. 15B.- 45C.1 D.- 15組卷:177引用:6難度:0.6
四、解答題:本題共6小題,第17題10分,第18-22題每題12分,共70分解答應(yīng)寫出文字說(shuō)明、證明過(guò)程或演算步驟.
-
21.已知等比數(shù)列{an}的前n項(xiàng)和為Sn,an+1=Sn+2(n∈N*).
(1)求數(shù)列{an}的通項(xiàng)公式;
(2)在an與an+1之間插入n個(gè)數(shù),使這n+2個(gè)數(shù)組成一個(gè)等差數(shù)列,記插入的這n個(gè)數(shù)之和為Tn,若不等式(-1)nλ<2-對(duì)一切n∈N*恒成立,求實(shí)數(shù)λ的取值范圍.2nTn組卷:64引用:1難度:0.6 -
22.已知函數(shù)
為自然對(duì)數(shù)的底數(shù))f(x)=alnxa-x,g(x)=ax-aex.(e=2.71828?
(1)當(dāng)a=1時(shí),求函數(shù)y=f(x)的最大值;
(2)已知x1,x2∈(0,+∞),且滿足f(x1)>g(x2),求證:.x1+aex2>2a組卷:107引用:6難度:0.3


