2022-2023學年廣西南寧市高二（下）調研數學試卷

一、選擇題：本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項符合題目要求.

• 1．已知A（3，2），B（-4，1），則直線AB的斜率為（　　）

  A． - 1 7

  B． 1 7

  C．-7

  D．7
  組卷：201引用：2難度：0.8

  解析

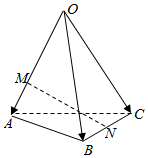• 2．如圖，空間四邊形OABC中，

  OA

  =

  a

  ，

  OB

  =

  b

  ，

  OC

  =

  c

  ，點M在

  OA

  上，且OM=2MA，點N為BC中點，則

  MN

  =（　　）

  A． 1 2 a - 2 3 b + 1 2 c	B． - 2 3 a + 1 2 b + 1 2 c
  C． 1 2 a + 1 2 b - 1 2 c	D． 2 3 a + 2 3 b - 1 2 c
  組卷：2455引用：155難度：0.9

  解析

• 3．已知A為拋物線C：y²=2px（p＞0）上一點，點A到C的焦點的距離為12，到y軸的距離為9，則p=（　　）

  A．2

  B．3

  C．6

  D．9
  組卷：7297引用：40難度：0.7

  解析

• 4．已知在等差數列{a_n}中，a₄+a₈=20，a₇=12，則a₄=（　　）

  A．12

  B．10

  C．6

  D．4
  組卷：379引用：10難度：0.8

  解析

• 5．點（3，0）到雙曲線

  x

  2

  16

  -

  y

  2

  9

  =1的一條漸近線的距離為（　　）

  A． 9 5

  B． 8 5

  C． 6 5

  D． 4 5
  組卷：3784引用：17難度：0.7

  解析

• 6．已知平面向量

  a

  ，

  b

  滿足|

  a

  |=1，|

  b

  |=2，且（

  a

  +

  b

  ）⊥

  a

  ，則

  a

  與

  b

  的夾角為（　　）

  A． 5 π 6

  B． 2 π 3

  C． π 3

  D． π 6
  組卷：83引用：20難度：0.9

  解析

• 7．如圖，正方形ABCD的邊長為5，取正方形ABCD各邊的中點E，F，G，H，作第2個正方形EFGH，然后再取正方形EFGH各邊的中點I，J，K，L，作第3個正方形IJKL，依此方法一直繼續下去．則從正方形ABCD開始，連續10個正方形的面積之和等于（　　）

  A． 50 [ 1 - （ 1 2 ） 10 ]	B． 25 [ 1 - （ 1 2 ） 10 ]
  C． 25 2 [ 1 - （ 1 2 ） 10 ]	D． 50 [ （ 1 2 ） 10 - 1 ]
  組卷：69引用：3難度：0.6

  解析

四、解答題：本題共6小題，共70分.解答應寫出文字說明、證明過程或演算步驟.

• 21．如圖，在三棱柱ABC-A₁B₁C₁中，側面BCC₁B₁為正方形，平面BCC₁B₁⊥平面ABB₁A₁，AB=BC=2，M，N分別為A₁B₁，AC的中點．
  （Ⅰ）求證：MN∥平面BCC₁B₁；
  （Ⅱ）再從條件①、條件②這兩個條件中選擇一個作為已知，求直線AB與平面BMN所成角的正弦值．
  條件①：AB⊥MN；
  條件②：BM=MN．
  注：如果選擇條件①和條件②分別解答，按第一個解答計分．
  組卷：4506引用：10難度：0.8

  解析

• 22．已知圓A：（x+2）²+y²=9，圓B：（x-2）²+y²=1，圓C與圓A、圓B外切．
  （1）求圓心C的軌跡方程E；
  （2）若過點B且斜率k的直線與E交于M、N兩點，線段MN的垂直平分線交x軸于點P，證明

  |

  MN

  |

  |

  PB

  |

  的值是定值．
  組卷：56引用：2難度：0.5

  解析