2023-2024學年江蘇省無錫市太湖高級中學高二（上）期中數學試卷

一、單選題（共8小題，每小題5分，共40分.在每小題列出的四個選項中，選出符合題目要求的一項.）

• 1．直線（a+1）x+3y+3=0與直線x+（a-1）y+1=0平行，則實數a的值為（　　）

  A．-2

  B． 1 2

  C．2

  D．2或-2
  組卷：211引用：9難度：0.5

  解析

• 2．已知點A，B，C不共線，對空間任意一點O，若

  OP

  =

  3

  4

  OA

  +

  1

  8

  OB

  +

  1

  8

  OC

  ，則P，A，B，C四點（　　）

  A．不共面

  B．共面

  C．不一定共面

  D．無法判斷
  組卷：175引用：8難度：0.8

  解析

• 3．已知向量

  a

  =

  （

  2

  3

  ，

  0

  ，

  2

  ）

  ，向量

  b

  =

  （

  1

  ，

  0

  ，

  3

  ）

  ，則向量

  a

  在向量

  b

  上的投影向量為（　　）

  A． （ 1 2 ， 0 ， 3 2 ）

  B． （ 2 3 ， 0 ， 2 ）

  C． （ 1 ， 0 ， 3 ）

  D． （ 3 ， 0 ， 3 ）
  組卷：98引用：2難度：0.7

  解析

• 4．若圓x²+y²+2x-4y+1=0被直線2ax-by+2=0（a＞0，b＞0）平分，則

  1

  a

  +

  1

  b

  的最小值為（　　）

  A． 1 4

  B．9

  C．4

  D． 1 9
  組卷：41引用：1難度：0.6

  解析

• 5．已知平行六面體ABCD-A₁B₁C₁D₁的所有棱長均為2，∠BAD=∠BAA₁=∠DAA₁=60°，M為C₁D₁的中點，則向量

  AM

  的模長為（　　）

  A． 15

  B．4

  C． 17

  D． 19
  組卷：33引用：2難度：0.7

  解析

• 6．已知A、B為橢圓

  x

  2

  4

  +

  y

  2

  3

  =

  1

  上兩點，O為坐標原點，M（異于點O）為弦AB中點，若AB兩點連線斜率為

  1

  2

  ，則OM兩點連線斜率為（　　）

  A． - 2 3

  B． - 3 2

  C． - 3 4

  D． - 4 3
  組卷：145引用：1難度：0.5

  解析

• 7．已知點P是圓M：（x-2）²+（y-2）²=2上的動點，線段AB是圓C：（x+1）²+（y+1）²=4的一條動弦，且

  |

  AB

  |

  =

  2

  3

  ，則

  |

  PA

  +

  PB

  |

  的最大值是（　　）

  A． 3 2

  B． 8 2

  C． 5 2

  D． 8 2 + 2
  組卷：288引用：9難度：0.4

  解析

四、解答題（共6小題，共70分。解答應寫出文字說明，演算步驟或證明過程.）

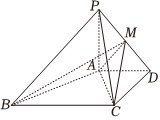• 21．如圖，在四棱錐P-ABCD中，PA⊥平面ABCD，AD∥BC，AD⊥CD，且AD=CD=2

  2

  ，BC=4

  2

  ，PA=2．
  （1）求證：AB⊥PC；
  （2）在線段PD上，是否存在一點M，使得平面MAC與平面PBC所成角的大小為30°，如果存在，求

  PM

  PD

  的值，如果不存在，請說明理由．
  組卷：106引用：1難度：0.5

  解析

• 22．已知P（0，1）為橢圓C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  上一點，長軸長為

  2

  2

  ．
  （1）求橢圓C的標準方程；
  （2）不經過點P的直線l與橢圓C相交于A，B兩點，若直線PA與PB的斜率之和為-1，證明：直線l必過定點，并求出這個定點坐標．
  組卷：154引用：1難度：0.5

  解析