2022-2023學(xué)年廣東省中山市紀(jì)念中學(xué)七年級(jí)（下）期中數(shù)學(xué)試卷

一、選擇題（本大題共10小題，每小題3分，共30分．）

• 1．下列各數(shù)中，屬于無(wú)理數(shù)的是（　　）

  A．0

  B．1.414

  C． 2

  D． 9
  組卷：81引用：5難度：0.9

  解析

• 2．點(diǎn)P的坐標(biāo)為（8，-3），則點(diǎn)P在（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  組卷：477引用：10難度：0.9

  解析

• 3．下列各式中是二元一次方程的是（　　）

  A．x+y=1

  B．x＞y

  C． 1 x + 2 = 3 y

  D．6xy+9=0
  組卷：108引用：3難度：0.5

  解析

• 4．下列圖形中，線段AD的長(zhǎng)表示點(diǎn)A到直線BC距離的是（　　）

  A．

  B．

  C．

  D．
  組卷：14686引用：102難度：0.9

  解析

• 5．如圖，△DEF是由△ABC通過(guò)平移得到，且點(diǎn)B，E，C，F(xiàn)在同一條直線上，若BF=14，EC=6，則BE的長(zhǎng)度是（　　）

  A．1

  B．2

  C．3

  D．4
  組卷：274引用：5難度：0.7

  解析

• 6．如圖，在下列給出的條件中，能判定DF∥AB的是（　　）

  A．∠4=∠3

  B．∠1=∠A

  C．∠1=∠4

  D．∠4+∠2=180°
  組卷：1070引用：21難度：0.7

  解析

• 7．實(shí)數(shù)n、m是連續(xù)整數(shù)，如果

  n

  ＜

  26

  ＜

  m

  ，那么m+n的值是（　　）

  A．7

  B．9

  C．11

  D．13
  組卷：609引用：4難度：0.7

  解析

五、解答題（三）（共2小題，每小題12分，滿分24分）

• 22．如圖，已知點(diǎn)A在EF上，點(diǎn)P，Q在BC上，∠E=∠EMA，∠BQM=∠BMQ．
  （1）求證：EF∥BC；
  （2）若FP⊥AC，∠2+∠C=90°，求證：∠1=∠B；
  （3）若∠3+∠4=180°，∠BAF=3∠F-20°，求∠B的度數(shù)．
  組卷：5260引用：14難度：0.3

  解析

• 23．如圖，在長(zhǎng)方形OABC中，O為平面直角坐標(biāo)系的原點(diǎn)，點(diǎn)A的坐標(biāo)為（a,0），點(diǎn)C的坐標(biāo)為（0，b）且a,b滿足

  a

  -

  8

  +

  |

  b

  -

  12

  |

  =

  0

  ，點(diǎn)B在第一象限內(nèi)，點(diǎn)P從原點(diǎn)出發(fā)，以每秒2個(gè)單位長(zhǎng)度的速度沿著O-A-B-C-O的線路移動(dòng)．
  （1）求點(diǎn)B的坐標(biāo)為

  ；當(dāng)點(diǎn)P移動(dòng)5秒時(shí)，點(diǎn)P的坐標(biāo)為

  ；
  （2）在移動(dòng)過(guò)程中，當(dāng)點(diǎn)P移動(dòng)11秒時(shí)，求△OPB的面積；
  （3）在（2）的條件下，坐標(biāo)軸上是否存在點(diǎn)Q，使△OPQ的面積與△OPB的面積相等，若存在，求點(diǎn)Q的坐標(biāo)；若不存在，說(shuō)明理由．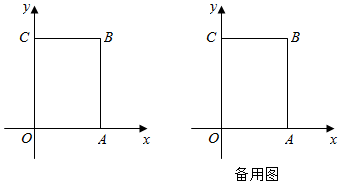
  
  組卷：1966引用：11難度：0.4

  解析