2023-2024學(xué)年遼寧省遼西聯(lián)合校高二（上）期中數(shù)學(xué)試卷

一、單項(xiàng)選擇題（共8小題，每小題5分，共40分，在每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)是符合題目要求的）

• 1．直線

  3

  x+y-2=0的傾斜角為（　　）

  A．30°

  B．150°

  C．120°

  D．60°
  組卷：379引用：11難度：0.9

  解析

• 2．兩平行直線3x-2y-1=0和6x-4y+3=0間的距離是（　　）

  A． 5 13 26

  B． 4 13 13

  C． 2 13 13

  D． 3 13 3
  組卷：298引用：17難度：0.9

  解析

• 3．已知直線l過圓x²+（y-3）²=4的圓心，且與直線x-y+1=0垂直，則l的方程是（　　）

  A．x+y-2=0

  B．x-y+2=0

  C．x-y+3=0

  D．x+y-3=0
  組卷：128引用：4難度：0.7

  解析

• 4．連接兩點(diǎn)的直線無限延展，與其平行的直線無論走多遠(yuǎn)都無法碰面．設(shè)m∈R，則“m=-1”是“直線mx+2y+4=0與直線x+（m-1）y+2=0平行”的（　　）

  A．充分必要條件	B．既不充分也不必要條件
  C．充分不必要條件	D．必要不充分條件
  組卷：15引用：4難度：0.8

  解析

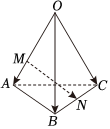• 5．如圖，在四面體OABC中，

  OA

  =

  a

  ，

  OB

  =

  b

  ，

  OC

  =

  c

  ．點(diǎn)M在OA上，且OM=2MA，N為BC中點(diǎn)，則

  MN

  等于（　　）

  A． 1 2 a - 2 3 b + 1 2 c	B． - 2 3 a + 1 2 b + 1 2 c
  C． 1 2 a + 1 2 b - 1 2 c	D． 2 3 a + 2 3 b - 1 2 c
  組卷：427引用：74難度：0.7

  解析

• 6．在下列命題中：
  ①若向量

  a

  ，

  b

  共線，則向量

  a

  ，

  b

  所在的直線平行；
  ②若向量

  a

  ，

  b

  所在的直線為異面直線，則向量

  a

  ，

  b

  一定不共面；
  ③若三個(gè)向量

  a

  ，

  b

  ，

  c

  兩兩共面，則向量

  a

  ，

  b

  ，

  c

  共面；
  ④已知是空間的三個(gè)向量

  a

  ，

  b

  ，

  c

  ，則對(duì)于空間的任意一個(gè)向量

  p

  總存在實(shí)數(shù)x,y,z使得

  p

  =

  x

  a

  +

  y

  b

  +

  z

  c

  ；
  其中正確的命題的個(gè)數(shù)是（　　）

  A．0

  B．1

  C．2

  D．3
  組卷：329引用：25難度：0.9

  解析

• 7．已知點(diǎn)F₁，F(xiàn)₂分別是橢圓

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  的左、右焦點(diǎn)，橢圓上的點(diǎn)到焦點(diǎn)的距離最大值為9，最小值為1．若點(diǎn)P在此橢圓上，∠F₁PF₂=60°，則△PF₁F₂的面積等于（　　）

  A． 3

  B． 3 3

  C． 6 3

  D． 9 3
  組卷：311引用：5難度：0.7

  解析

四、解答題（本題共6小題，滿分70分，答題時(shí)必須寫文字說明、證明過程或者演算步驟）

• 21．如圖在四棱錐P-ABCD中，側(cè)面PAD⊥底面ABCD，側(cè)棱PA=PD=

  2

  ，底面ABCD為直角梯形，其中BC∥AD，AB⊥AD，AD=2AB=2BC=2，O為AD的中點(diǎn)．
  （1）求證：PO⊥平面ABCD；
  （2）求二面角C-PD-A夾角的正弦值；
  （3）線段AD上是否存在Q，使得它到平面PCD的距離為

  3

  2

  ？若存在，求出

  AQ

  QD

  的值；若不存在，說明理由．
  組卷：189引用：5難度：0.4

  解析

• 22．已知定圓F：（x-1）²+y²=16，動(dòng)圓H過點(diǎn)E（-1，0）且與圓F相切，記圓心H的軌跡為C．
  （1）求曲線C的方程．
  （2）已知A（-2，0），B（2，0），點(diǎn)M是曲線C上異于A、B的任意一點(diǎn)，設(shè)直線AM與直線l：x=4交于點(diǎn)N，求證：∠MFB=2∠NFB．
  組卷：27引用：2難度：0.5

  解析