2022-2023學(xué)年河南省南陽(yáng)市宛城區(qū)金華中學(xué)八年級(jí)（上）第一次月考數(shù)學(xué)試卷

一、選擇題（共30分）

• 1．小明在作業(yè)本上做了4道題①

  3

  -

  125

  =-5；②±

  16

  =4；③

  3

  81

  =9；④

  （

  -

  6

  ）

  2

  =-6，他做對(duì)的題有（　　）

  A．1道

  B．2道

  C．3道

  D．4道
  組卷：809引用：16難度：0.8

  解析

• 2．下列說(shuō)法錯(cuò)誤的是（　　）

  A．3的平方根是 3

  B．-1的立方根是-1

  C．0.1是0.01的一個(gè)平方根

  D．算術(shù)平方根是本身的數(shù)只有0和1
  組卷：1877引用：17難度：0.9

  解析

• 3．下列各式中，計(jì)算正確的是（　　）

  A．a(chǎn)3+a2=a5

  B．a(chǎn)3-a2=a

  C．（a2）3=a5

  D．a(chǎn)2?a3=a5
  組卷：774引用：28難度：0.7

  解析

• 4．已知3^2m=5，3²ⁿ=10，則9^m-n+1的值是（　　）

  A． 9 2

  B． 3 2

  C．-2

  D．4
  組卷：1988引用：16難度：0.6

  解析

• 5．電子文件的大小常用B，KB，MB，GB等作為單位，其中1GB=2¹⁰MB，1MB=2¹⁰KB，1KB=2¹⁰B．某視頻文件的大小約為1GB，1GB等于（　　）

  A．230B

  B．830B

  C．8×1010B

  D．2×1030B
  組卷：3574引用：41難度：0.8

  解析

• 6．若單項(xiàng)式-3x^4a-by²與

  1

  3

  x

  3

  y

  a

  +

  b

  是同類項(xiàng)，那么這兩個(gè)單項(xiàng)式的積是（　　）

  A．x6y4

  B．-x3y2

  C．- 8 3 x 3 y 2

  D．-x6y4
  組卷：410引用：4難度：0.5

  解析

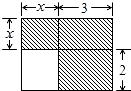• 7．下面四個(gè)整式中，不能表示圖中陰影部分面積的是（　　）

  A．x2+5x	B．x（x+3）+6
  C．3（x+2）+x2	D．（x+3）（x+2）-2x
  組卷：9348引用：116難度：0.7

  解析

三、解答題（共75分）

• 22．（1）比較下列兩個(gè)算式的結(jié)果的大小（在橫線上選填“＞”“=”或“＜”）
  ①3²+4²

  2×3×4；
  ②（

  1

  3

  ）²+（

  1

  4

  ）²

  2×

  1

  3

  ×

  1

  4

  ；
  ③（-2）²+（-3）²

  2×（-2）×（-3）；
  ④（-4）²+（-4）²

  2×（-4）×（-4）…
  （2）觀察并納（1）中的規(guī)律，用含a,b的一個(gè)關(guān)系式把你的發(fā)現(xiàn)表示出來(lái)．
  組卷：17引用：3難度：0.7

  解析

• 23．材料1：著名的瑞士數(shù)學(xué)家歐拉曾指出：可以表示為四個(gè)整數(shù)平方之和的甲、乙兩數(shù)相乘，其乘積仍然可以表示為四個(gè)整數(shù)平方之和，即（a²+b²+c²+d²）（e²+f²+g²+h²）=A²+B²+C²+D²，這就是著名的歐拉恒等式，有人稱這樣的數(shù)為“不變心的數(shù)”．
  實(shí)際上，上述結(jié)論可減弱為：可以表示為兩個(gè)整數(shù)平方之和的甲、乙兩數(shù)相乘，其乘積仍然可以表示為兩個(gè)整數(shù)平方之和，即（a²+b²）（c²+d²）=A²+B²
  材料2：在數(shù)學(xué)思想中，有種解題技巧稱之為“無(wú)中生有”．
  例如問(wèn)題：將代數(shù)式x²-y²+

  1

  x

  2

  -

  1

  y

  2

  改成兩個(gè)平方之和的形式．
  解：原式=（x²+

  1

  x

  2

  +2?x?

  1

  x

  ）-（y²+

  1

  y

  2

  +2?y?

  1

  y

  ）=（x+

  1

  x

  ）²-（y+

  1

  y

  ）²．
  解決問(wèn)題：
  （1）試將（1²+2²）（1²+3²）改寫成兩個(gè)不相等的整數(shù)平方之和的形式．（1²+2²）（1²+3²）=

  ；
  （2）請(qǐng)你靈活運(yùn)用“無(wú)中生有”的解題技巧解決“不變心的數(shù)”問(wèn)題：將代數(shù)式（a²+b²）（c²+d²）改成兩個(gè)整數(shù)平方之和的形式（其中a、b、c、d均為整數(shù)），并給出詳細(xì)的推導(dǎo)過(guò)程．
  組卷：32引用：2難度：0.6

  解析