2022-2023學年湖南省長沙市長郡中學高一（下）第一次適應性數學試卷

一、選擇題（本題共8小題，每小題5分，共40分．在每個小題給出的四個選項中，只有一項符合題目要求．）

• 1．已知復數z滿足z=3-i（其中i為虛數單位），則|z|=（　　）

  A． 5

  B． 10

  C．4

  D． 10 2
  組卷：56引用：6難度：0.8

  解析

• 2．△ABC的三內角A，B，C所對邊分別為a,b,c,若a²+b²-c²=ab,則角C的大小為（　　）

  A． π 6

  B． π 3

  C． π 2

  D． 2 π 3
  組卷：540引用：16難度：0.9

  解析

• 3．已知平面向量

  a

  =

  （

  sinθ

  ，

  1

  ）

  ，

  b

  =

  （

  cosθ

  ，-

  2

  ）

  ，若

  a

  ∥

  b

  ，則tanθ=（　　）

  A． - 1 2

  B．-2

  C．2

  D． 1 2
  組卷：585引用：10難度：0.8

  解析

• 4．函數

  f

  （

  x

  ）

  =

  xcosx

  e

  |

  x

  |

  的圖象大致為（　　）

  A．	B．
  C．	D．
  組卷：256引用：9難度：0.7

  解析

• 5．已知正實數a,b滿足a+2b=1，則

  1

  a

  +

  8

  b

  的最小值為（　　）

  A．8

  B．17

  C．20

  D．25
  組卷：923引用：4難度：0.7

  解析

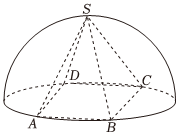• 6．如圖，半球內有一內接正四棱錐S-ABCD，該四棱錐的體積為

  4

  2

  3

  ，則該半球的體積為（　　）

  A． 2 3 π

  B． 4 2 9 π

  C． 4 2 3 π

  D． 8 2 3 π
  組卷：210引用：6難度：0.6

  解析

• 7．已知f（x）是偶函數且在[0，+∞）上單調遞增，則滿足f（sinx）＜f（cosx）的一個區間是（　　）

  A． （ π 4 ， π 2 ）

  B． （ 3 π 4 ， π ）

  C． （ - 5 π 4 ， 3 π 2 ）

  D． （ 3 π 2 ， 7 π 4 ）
  組卷：38引用：4難度：0.6

  解析

四、解答題（本題共6小題，共70分．解答應寫出文字說明、證明過程或演算步驟．）

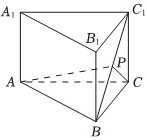• 21．如圖，直三棱柱ABC-A₁B₁C₁中，BC=AA₁=1，

  AB

  =

  2

  ，

  cos

  ∠

  ACB

  =

  3

  3

  ，P為線段BC₁上的動點．
  （1）當P為線段BC₁上的中點時，求三棱錐B-PAC的體積；
  （2）當P在線段BC₁上移動時，求AP+CP的最小值．
  組卷：356引用：8難度：0.4

  解析

• 22．定義非零向量

  OM

  =（a,b）的“相伴函數”為f（x）=asinx+bcosx（x∈R），向量

  OM

  =（a,b）稱為函數f（x）=asinx+bcosx（x∈R）的“相伴向量”（其中O為坐標原點）．記平面內所有向量的“相伴函數”構成的集合為S．
  （1）設h（x）=

  3

  cos（x+

  π

  6

  ）+3cos（

  π

  3

  -x）（x∈R），請問函數h（x）是否存在相伴向量

  OM

  ，若存在，求出與

  OM

  共線的單位向量；若不存在，請說明理由．
  （2）已知點M（a,b）滿足：

  b

  a

  ∈

  （

  0

  ，

  3

  ]，向量

  OM

  的“相伴函數”f（x）在x=x₀處取得最大值，求tan2x₀的取值范圍．
  組卷：403引用：8難度：0.1

  解析