當前位置：試卷中心 > 試卷詳情

北師大新版八年級數學上冊《第1章勾股定理》2016年單元測試卷（2）

發布：2024/11/17 19:0:1

1．△ABC中∠A、∠B、∠C的對邊分別是a、b、c,下列命題中的假命題是（　　）

A．如果∠C-∠B=∠A，則△ABC是直角三角形

B．如果c²=b²-a²，則△ABC是直角三角形，且∠C=90°

C．如果（c+a）（c-a）=b²，則△ABC是直角三角形

D．如果∠A：∠B：∠C=5：2：3，則△ABC是直角三角形

組卷：2992引用：46難度：0.9

2．下列各組數的三個數，可作為三邊長構成直角三角形的是（　　）
A．1，2，3 B．3²，4²，5²
C．
1
3
，
1
4
，
1
5
D．0.3，0.4，0.5
組卷：554引用：4難度：0.9
解析
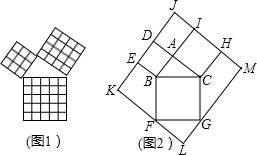3．勾股定理是幾何中的一個重要定理．在我國古算書《周髀算經》中就有“若勾三，股四，則弦五”的記載．如圖1是由邊長相等的小正方形和直角三角形構成的，可以用其面積關系驗證勾股定理．圖2是由圖1放入矩形內得到的，∠BAC=90°，AB=3，AC=4，點D，E，F，G，H，I都在矩形KLMJ的邊上，則矩形KLMJ的面積為（　　）
A．90 B．100 C．110 D．121
組卷：7099引用：72難度：0.9
解析
4．在Rt△ABC中，斜邊長BC=3，AB²+AC²+BC²的值為（　　）
A．18 B．9 C．6 D．無法計算
組卷：641引用：8難度：0.9
解析
5．在Rt△ABC中，a,b,c為△ABC三邊長，則下列關系正確的是（　　）
A．a²+b²=c² B．a²+c²=b²
C．b²+c²=a² D．以上關系都有可能
組卷：409引用：3難度：0.9
解析

14．如圖，在長方形紙片ABCD中，AB=18，把長方形紙片沿直線AC折疊，點B落在點E處，AE交DC于點F，若AF=13，求AD的長．
組卷：1086引用：2難度：0.3
解析
15．如圖，對任意符合條件的直角三角形BAC，繞其銳角頂點逆時針旋轉90°得△DAE，所以∠BAE=90°，且四邊形ACFD是一個正方形，它的面積和四邊形ABFE面積相等，而四邊形ABFE面積等于Rt△BAE和Rt△BFE的面積之和，根據圖形寫出一種證明勾股定理的方法．
組卷：1274引用：5難度：0.3
解析