2022-2023學年廣東省茂名一中奧林匹克學校高二(下)期中數學試卷
發布:2024/6/2 8:0:8
一、選擇題(每小題5分,共8小題40分)
-
1.已知集合
,則A∩B=( )A={x|log2(x+1)≤2},B={x|x2-x+2x>0}A.{x|2<x≤3} B.{x|x≤3} C.{x|-1<x≤3} D.{x|0<x≤3} 組卷:132引用:3難度:0.7 -
2.“m=1”是“函數
為奇函數”的( )f(x)=2x+m2x-mA.充分不必要條件 B.必要不充分條件 C.充要條件 D.既不充分也不必要條件 組卷:392引用:4難度:0.7 -
3.已知函數f(x)=ex-lg|x|,則f(x)的圖象大致為( )
A. 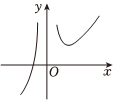
B. 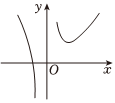
C. 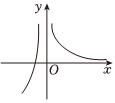
D. 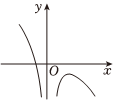 組卷:174引用:7難度:0.6
組卷:174引用:7難度:0.6 -
4.已知
則( )a=cos1,p=loga12,q=a12,r=(12)aA.p<q<r B.p<r<q C.r<q<p D.q<p<r 組卷:144引用:2難度:0.6 -
5.若函數f(x)=
的圖象關于原點對稱,且f(5)=1,則h(-2022)+h(-2023)+h(-2024)=( )f(x+2),x≥0h(x),x<0A.-1 B.0 C.1 D.2 組卷:169引用:3難度:0.7 -
6.定義函數迭代:
f(0)(x)=x
f(1)(x)=f(x)
f(2)(x)=f(f(x))
?
f(n+1)(x)=f(f(n)(x))
已知f(x)=3x+2,則f(n)(x)=( )A.3nx+3n-1 B.3nx+3n+1 C.3nx+3n-1 D.3nx-3n+1 組卷:51引用:3難度:0.6 -
7.如果方程
所對應的曲線與函數y=f(x)對的圖像完全重合,那么對于函數y=f(x)有如下兩個結論:x24+y|y|=1
①函數f(x)的值域為(-∞,2];
②函數F(x)=f(x)+x有且只有一個零點.
對這兩個結論,以下判斷正確的是( )A.①正確,②錯誤 B.①錯誤,②正確 C.①②都正確 D.①②都錯誤 組卷:88引用:4難度:0.5
四、解答題(共6小題70分)
-
21.已知橢圓E:
=1(a>b>0)過點x2a2+y2b2.A(1,32)
(1)若橢圓E的離心率,求b的取值范圍;e∈(0,12]
(2)已知橢圓E的離心率e=,M,N為橢圓E上不同兩點,若經過M,N兩點的直線與圓x2+y2=b2相切,求線段MN的最大值.32組卷:170引用:4難度:0.4 -
22.已知函數f(x)=sinx-(x+2)e-x.
(Ⅰ)證明:函數f(x)在區間[0,π]上有2個零點;
(Ⅱ)若函數g(x)=ax+sinx-f(x)(a∈R)有兩個極值點:x1,x2,且x1<x2.求證:(其中e=2.71828…為自然對數的底數)0<x1+x2<2-2aa組卷:104引用:3難度:0.3


