當(dāng)前位置：試卷中心 > 試卷詳情

2022-2023學(xué)年山東省德州市高一（下）期中數(shù)學(xué)試卷

發(fā)布：2024/7/19 8:0:9

一、選擇題（本題共8個(gè)小題，每小題5分，共40分．在每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)是符合要求的．）

1．在復(fù)平面內(nèi)，復(fù)數(shù)z對(duì)應(yīng)的點(diǎn)的坐標(biāo)是（-2，1），則zi的虛部為（　　）
A．2i B．2 C．-2i D．-2
組卷：49引用：4難度：0.8
解析
2．已知
AB
=
（
2
，
3
）
，
AC
=
（
3
，
t
）
，
AB
⊥
BC
，則t=（　　）
A．
7
3
B．
9
2
C．
3
7
D．-3
組卷：82引用：3難度：0.7
解析
3．已知
cos
2
α
sin
（
α
-
π
4
）
=
-
6
2
，則
cos
（
α
-
π
4
）
=（　　）
A．
2
4
B．
-
2
4
C．
-
6
4
D．
6
4
組卷：224引用：4難度：0.8
解析
4．已知
a
=
（
-
2
，
1
）
，
b
=
（
-
2
，-
3
）
，則
b
在
a
上的投影向量是（　　）
A．
（
-
2
13
13
，-
3
13
13
）
B．
（
-
2
5
，
1
5
）
C．
（
-
2
13
13
，
3
13
13
）
D．
（
2
5
，-
1
5
）
組卷：97引用：3難度：0.8
解析
5．在△ABC中，BC=5，D為BC上一點(diǎn)，且2BD=3DC，若
AB
=
3
AC
=
3
AD
，則AD的長(zhǎng)度為（　　）
A．
5
B．
15
C．
30
2
D．3
組卷：94引用：2難度：0.7
解析
6．已知平行四邊形ABCD中，
|
AB
|
=
8
，
|
AD
|
=
4
，
∠
A
=
π
3
．若點(diǎn)M滿足
AM
=
1
5
MB
，點(diǎn)N為AB中點(diǎn)，則
DM
?
（
DA
+
DN
）
=（　　）
A．6 B．12 C．24 D．30
組卷：77引用：2難度：0.6
解析
7．三國(guó)時(shí)期的數(shù)學(xué)家劉徽在對(duì)《九章算術(shù)》作注時(shí)，給出了“割圓術(shù)”求圓周率的方法；魏晉南北朝時(shí)期，祖沖之利用割圓術(shù)求出圓周率π約為
355
113
，這一數(shù)值與π的誤差小于八億分之一．現(xiàn)已知π的近似值還可表示為4sin52°，則
2
π
16
-
π
2
-
8
sin
44
°
3
-
2
3
sin
2
22
°
的值為（　　）
A．
-
8
3
B．-8 C．8 D．
8
3
組卷：145引用：2難度：0.5
解析

當(dāng)前模式為游客模式，立即登錄查看試卷全部?jī)?nèi)容及下載

四、解答題（本題共6小題，共70分．解答應(yīng)寫出必要的文字說(shuō)明、證明過(guò)程或演算步驟．）

21．已知O為坐標(biāo)原點(diǎn)，對(duì)于函數(shù)f（x）=asinx+bcosx,稱向量
OM
=
（
a
,
b
）
為函數(shù)f（x）的伴隨向量，同時(shí)稱函數(shù)f（x）為向量
OM
的伴隨函數(shù)．
（1）設(shè)函數(shù)
g
（
x
）
=
4
cos
（
x
2
+
π
3
）
?
cos
x
2
-
1
，試求g（x）的伴隨向量
OM
；
（2）將（1）中函數(shù)g（x）的圖象向右平移
π
3
個(gè)單位長(zhǎng)度，再把整個(gè)圖象橫坐標(biāo)伸長(zhǎng)為原來(lái)的2倍（縱坐標(biāo)不變）得到h（x）的圖象，已知A（-2，3），B（2，6），問(wèn)在y=h（x）的圖象上是否存在一點(diǎn)P，使得
AP
⊥
BP
．若存在，求出P點(diǎn)坐標(biāo)；若不存在，說(shuō)明理由．
組卷：66引用：3難度：0.5
解析
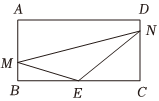22．某公園有一塊長(zhǎng)方形空地ABCD，如圖，AB=2，AD=4．為迎接“五一”觀光游，在邊界BC上選擇中點(diǎn)E，分別在邊界AB、CD上取M、N兩點(diǎn)，現(xiàn)將三角形地塊MEN修建為花圃，并修建觀賞小徑EM，EN，MN，且
∠
MEN
=
2
3
π
．
（1）當(dāng)
∠
BEM
=
π
6
時(shí)，求花圃的面積；
（2）求觀賞小徑EM與EN長(zhǎng)度和的取值范圍．
組卷：60引用：4難度：0.5
解析