2021年貴州省黔南州甕安中學高考數學關門考試試卷（文科）

一、選擇題：（本題共12小題，每小題5分，共60分）.

• 1．已知集合A={x|-1＜x＜2}，B={x|x＞1}，則A∪B=（　　）

  A．（-1，1）

  B．（1，2）

  C．（-1，+∞）

  D．（1，+∞）
  組卷：2756引用：23難度：0.9

  解析

• 2．已知z=

  3

  -

  i

  1

  -

  i

  （其中i為虛數單位），則

  z

  的虛部為（　　）

  A．-i

  B．-1

  C．1

  D．2
  組卷：159引用：7難度：0.8

  解析

• 3．等比數列{a_n}中，若a₄=8a₁，且a₁，a₂+1，a₃成等差數列，則其前5項和為（　　）

  A．30

  B．32

  C．62

  D．64
  組卷：240引用：7難度：0.7

  解析

• 4．已知向量|

  a

  |=2，|

  b

  |=1，

  a

  ?（

  a

  -2

  b

  ）=2，則

  a

  與

  b

  的夾角為（　　）

  A．30°

  B．60°

  C．90°

  D．150°
  組卷：403引用：8難度：0.8

  解析

• 5．已知雙曲線

  x

  2

  a

  2

  -y²=1（a＞0）的離心率是

  5

  ，則a=（　　）

  A． 6

  B．4

  C．2

  D． 1 2
  組卷：3138引用：18難度：0.7

  解析

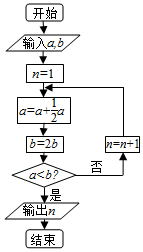• 6．數學名著《算學啟蒙》中有關于“松竹并生”的問題：松長四尺，竹長兩尺，松日自半，竹日自倍，松竹何日而長等．如圖，是源于其思想的一個程序框圖．若輸入的a,b分別為8、2，則輸出的n=（　　）

  A．2

  B．3

  C．5

  D．4
  組卷：79引用：6難度：0.9

  解析

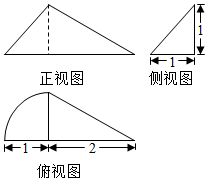• 7．已知一個幾何體的三視圖如圖所示，則該幾何體的表面積為（　　）

  A． 4 + 1 2 π	B． 5 + 10 2 + 1 2 π
  C． 5 + 10 2 + 1 + 2 4 π	D． 4 + 1 + 2 4 π
  組卷：227引用：11難度：0.7

  解析

（二）選考題：共10分.請考生在第22，23題中任選一題作答，如果多做，則按所做的第一題計分.[選修4–4：坐標系與參數方程]（10分）

• 22．在平面直角坐標系xOy中，曲線C₁的參數方程為

  x = - 2 + cosα

  y = 2 + sinα

  （α為參數）以坐標原點為極點，x軸的非負半軸為極軸建立極坐標系，曲線C₂的極坐標方程為

  ρ

  （

  sinθ

  -

  3

  cosθ

  ）

  =

  1

  ．
  （Ⅰ）分別求曲線C₁的普通方程和曲線C₂的直角坐標方程；
  （Ⅱ）若P，Q分別是曲線C₁和C₂上的動點，求|PQ|的最小值．
  組卷：120引用：3難度：0.7

  解析

[選修4–5：不等式選講]（10分）

• 23．已知函數f（x）=|x-a|+|x-a²|．
  （Ⅰ）當a=-1時，求f（x）≤4的解集；
  （Ⅱ）記f（x）的最小值為g（a），求g（a）在a∈[0，2]時的最大值．
  組卷：86引用：4難度：0.5

  解析