當前位置：試卷中心 > 試卷詳情

2022-2023學年北京市通州區運河中學高二（上）月考數學試卷（10月份）

發布：2024/9/20 10:0:8

1．在長方體ABCD-A₁B₁C₁D₁中，
BA
+
BC
+
D
D
1
=（　　）
A．
D
1
B
1
B．
D
1
B
C．
D
B
1
D．
B
D
1
組卷：801引用：12難度：0.7
解析
2．已知向量
a
=（2，-3，1），
b
=（2，0，3），則
a
?（
a
+
b
）=（　　）
A．21 B．-21 C．20 D．-20
組卷：544引用：3難度：0.9
解析
3．若向量
a
=（1，2，0），
b
=（-2，0，1），則（　　）
A．cos＜
a
，
b
＞=-
2
5
B．
a
⊥
b
C．
a
∥
b
D．|
a
|=|
b
|
組卷：303引用：14難度：0.9
解析
4．已知空間向量
a
=（2，1，-1），
b
=（x,-2，2），且
a
∥
b
，則x=（　　）
A．-2 B．-4 C．2 D．4
組卷：46引用：4難度：0.8
解析
5．已知直線l₁，l₂的方向向量分別為
a
=（1，2，-2），
b
=（-2，1，m），若l₁⊥l₂，則m等于（　　）
A．1 B．2 C．0 D．3
組卷：125引用：3難度：0.8
解析
6．已知M為z軸上一點，且點M到點A（-1，0，1）與點（1，-3，2）的距離相等，則點M的坐標為（　　）
A．（3，0，0） B．（0，-2，0） C．（0，0，6） D．（0，0，-3）
組卷：554引用：2難度：0.8
解析
7．已知{
a
，
b
，
c
}是空間向量的一個基底，則下列向量中能與
a
+
b
，
a
-
b
構成基底的是（　　）
A．
a
B．
b
C．
c
D．
a
+2
b
組卷：46引用：4難度：0.8
解析

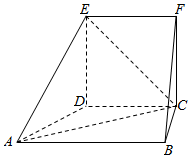22．在如圖所示的幾何體中，四邊形CDEF為正方形，四邊形ABCD為直角梯形，AB∥CD，BC⊥CD，BC⊥CF，AB=3BC=3CD．
（1）求BE與平面EAC所成角的正弦值；
（2）線段ED或其延長線上是否存在點P，使平面EAC⊥平面PBC？證明你的結論．
組卷：67引用：4難度：0.6
解析
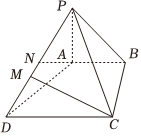23．如圖，在四棱錐P-ABCD中，PA⊥面ABCD，AB∥CD，且CD=2，AB=1，
BC
=
2
2
，PA=1，AB⊥BC，N為PD的中點．
（Ⅰ）求直線AN到平面PBC的距離；
（Ⅱ）在線段PD上是否存在一點M，使得直線CM與平面PBC所成角的正弦值是
1
3
，若存在，求出
DM
DP
的值，若不存在，說明理由．
組卷：14引用：1難度：0.5
解析