2022-2023學年北京二中高二（下）期末數學試卷

一、選擇題（共10小題，每小題5分，共5分．選出符合題目要求的一項）

• 1．集合A={x∈R|x≤2}，B={x∈R|x²-3x≤0}，則（?_RA）∩B=（　　）

  A．{x|0≤x≤2}

  B．{x|2＜x≤3}

  C．{x|2≤x≤3}

  D．{x|x＞0}
  組卷：147引用：4難度：0.8

  解析

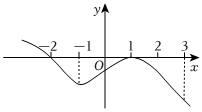• 2．已知函數f（x）的導函數f′（x）的圖象如圖所示，則下列結論中正確的是（　　）

  A．f（x）在區間（-2，3）上有2個極值點

  B．f（x）在x=-1處取得極小值

  C．f（x）在區間（-2，3）上單調遞減

  D．f（x）在x=1處取得極大值
  組卷：303引用：3難度：0.7

  解析

• 3．已知函數f（x）=x²+bx+c,b,c∈R，則“c＜0”是“函數f（x）有零點”的（　　）

  A．充分而不必要條件	B．必要而不充分條件
  C．充分必要條件	D．既不充分也不必要條件
  組卷：150引用：3難度：0.7

  解析

• 4．一個盒子里有3個分別標有號碼為1，2，3的小球，每次取出一個，記下它的標號后再放回盒子中，共取3次，則取得小球標號最大值是3的取法有（　　）

  A．12種

  B．15種

  C．17種

  D．19種
  組卷：360引用：11難度：0.7

  解析

• 5．

  （

  x

  2

  -

  1

  2

  x

  ）

  5

  的展開式中x的系數是（　　）

  A．10

  B． - 5 2

  C． 5 4

  D． - 5 4
  組卷：393引用：6難度：0.8

  解析

• 6．從甲、乙等5名志愿者中選出4名，分別從事A，B，C，D四項不同的工作，每人承擔一項．甲不從事A工作的概率為（　　）

  A． 7 10

  B． 4 5

  C． 3 5

  D． 1 5
  組卷：269引用：2難度：0.5

  解析

• 7．已知數列{a_n}中，a₁=2，a_n+1-2a_n=0，b_n=log₂a_n，那么數列{b_n}的前10項和等于（　　）

  A．130

  B．120

  C．55

  D．50
  組卷：378引用：18難度：0.7

  解析

三、解答題（共6小題，共75分．解答應寫出文字說明，演算步驟或證明過程）

• 20．函數

  f

  （

  x

  ）

  =

  1

  2

  x

  2

  -

  alnx

  +

  b

  （

  a

  ∈

  R

  ）

  ．
  （1）若曲線y=f（x）在x=1處的切線的方程為3x-y-3=0，求實數a、b的值；
  （2）討論函數f（x）的單調性；
  （3）若a=-2，對任意x₁，x₂∈（0，2]，不等式

  |

  f

  （

  x

  1

  ）

  -

  f

  （

  x

  2

  ）

  |

  ≤

  m

  |

  1

  x

  1

  -

  1

  x

  2

  |

  恒成立，求m的最小值．
  組卷：269引用：2難度：0.3

  解析

• 21．已知集合M={1，2，3，…，n}（n∈N^*），若集合

  A

  =

  {

  a

  1

  ，

  a

  2

  ，

  a

  3

  ，…，

  a

  m

  }

  （

  m

  ∈

  N

  *

  ）

  ，且對任意的b∈M，存在a_i，a_j∈A（1≤i≤j≤m），使得b=λ₁a_i+λ₂a_j（其中λ₁，λ₂∈{-1，0，1}），則稱集合A為集合M的一個m元基底．
  （Ⅰ）分別判斷下列集合A是否為集合M的一個二元基底，并說明理由；
  ①A={1，5}M={1，2，3，4，5}；
  ②A={2，3}，M={1，2，3，4，5，6}．
  （Ⅱ）若集合A是集合M的一個m元基底，證明：m（m+1）≥n；
  （Ⅲ）若集合A為集合M={1，2，3，…，19}的一個m元基底，求出m的最小可能值，并寫出當m取最小值時M的一個基底A．
  組卷：137引用：6難度：0.1

  解析