2023-2024學(xué)年四川省成都外國(guó)語學(xué)校高二（上）月考數(shù)學(xué)試卷（10月份）

一、單項(xiàng)選擇題：本大題共8小題，每小題5分，共40分．在每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)是符合題目要求的．

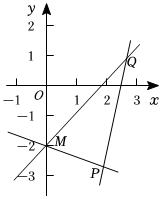• 1．如圖，已知直線PM、QP、QM的斜率分別為k₁、k₂、k₃，則k₁、k₂、k₃的大小關(guān)系為（　　）

  A．k1＜k3＜k2

  B．k1＜k2＜k3

  C．k2＜k1＜k3

  D．k3＜k2＜k1
  組卷：287引用：7難度：0.7

  解析

• 2．緡云山是著名的旅游勝地．天氣預(yù)報(bào)中秋節(jié)連續(xù)三天，每天下雨的概率為0.5，現(xiàn)用隨機(jī)模擬的方法估計(jì)三天中至少有兩天下雨的概率：先由計(jì)算器產(chǎn)生0到9之間的整數(shù)值的隨機(jī)數(shù)，指定0，1，2，3，4表示當(dāng)天下雨，5，6，7，8，9表示當(dāng)天不下雨，每3個(gè)隨機(jī)數(shù)為一組，代表三天是否下雨的結(jié)果，經(jīng)隨機(jī)模擬產(chǎn)生了20組隨機(jī)數(shù)：
  926   446   072   021   392   077   663   817   325   615
  405   858   776    631   700   259   305   311   589   258
  據(jù)此估計(jì)三天中至少有兩天下雨的概率約為（　　）

  A．0.45

  B．0.5

  C．0.55

  D．0.6
  組卷：65引用：2難度：0.8

  解析

• 3．已知直線ax+2y+6=0與直線x+（a-1）y+a²-1=0互相平行，則實(shí)數(shù)a的值為（　　）

  A．-2

  B．2或-1

  C．2

  D．-1
  組卷：565引用：8難度：0.8

  解析

• 4．現(xiàn)從2個(gè)男生2個(gè)女生共4人中任意選出2人參加巴蜀中學(xué)高三年級(jí)的百日誓師大會(huì)，已知選出的2人中有一個(gè)是男生，則另一個(gè)是女生的概率為（　　）

  A． 1 2

  B． 2 3

  C． 4 5

  D． 5 6
  組卷：209引用：7難度：0.7

  解析

• 5．△ABC中，D為AB上一點(diǎn)且滿足

  AD

  =

  1

  2

  DB

  ，若P為線段CD上一點(diǎn)，且滿足

  AP

  =

  λ

  AB

  +

  μ

  AC

  （λ，μ為正實(shí)數(shù)），則

  1

  3

  λ

  +

  1

  μ

  的最小值為（　　）

  A．3

  B．4

  C．5

  D．6
  組卷：322引用：5難度：0.7

  解析

• 6．數(shù)學(xué)家歐拉在1765年提出定理：三角形的外心，重心，垂心依次位于同一直線上，且重心到外心的距離是重心到垂心距離的一半．這條直線被后人稱為三角形的歐拉線．已知△ABC的頂點(diǎn)A（2，0），B（0，1），且AC=BC，則△ABC的歐拉線的方程為（　　）

  A．2x+4y-3=0

  B．x-2y-3=0

  C．2x-y-3=0

  D．4x-2y-3=0
  組卷：102引用：2難度：0.7

  解析

• 7．在如圖所示的電路中，5個(gè)盒子表示保險(xiǎn)匣，設(shè)5個(gè)盒子被斷開分別為事件A，B，C，D，E．盒子中所示數(shù)值表示通電時(shí)保險(xiǎn)絲被切斷的概率，下列結(jié)論正確的是（　　）

  A．A，B兩個(gè)盒子串聯(lián)后暢通的概率為 1 6

  B．D，E兩個(gè)盒子并聯(lián)后暢通的概率為 1 15

  C．A，B，C三個(gè)盒子混聯(lián)后暢通的概率為 1 2

  D．當(dāng)開關(guān)合上時(shí)，整個(gè)電路暢通的概率為 7 9
  組卷：86引用：4難度：0.7

  解析

四、解答題：第17題10分，第18～22題每道題12分，共計(jì)70分．解答應(yīng)寫出相應(yīng)的文字說明、證明過程或者演算步驟．

• 21．在銳角△ABC中，角A，B，C所對(duì)的邊分別為a,b,c,bsinA+atanAcosB=2asinC．
  （1）求A；
  （2）若D為BC延長(zhǎng)線上一點(diǎn)，且

  ∠

  CAD

  =

  π

  4

  ，求

  BC

  CD

  的取值范圍．
  組卷：151引用：5難度：0.5

  解析

• 22．如圖，四邊形ABCD與BDEF均為菱形，AB=2，

  ∠

  DAB

  =

  π

  3

  ，

  FA

  =

  FC

  =

  6

  ，記平面AEF與平面ABCD的交線為l.
  （1）證明：BD∥l；
  （2）證明：平面BDEF⊥平面ABCD；
  （3）記平面AEF與平面ABCD夾角為α，若正實(shí)數(shù)m,n滿足

  mco s 2 θ = sinθ - tcosθ

  nsi n 2 θ = cosθ + tsinθ

  ，

  0

  ＜

  θ

  ＜

  π

  2

  ，證明：

  m

  +

  n

  ＞

  3

  3

  2

  tanα

  ．
  組卷：121引用：6難度：0.4

  解析