2023-2024學年天津市南開區高三（上）期中數學試卷

一、選擇題：在每小題給出的四個選項中，只有一項是符合題目要求的。

• 1．已知全集U={-1，0，1，2，3}，A={-1，1}，B={x|x≤-1或x≥2}，則A∪（?_UB）=（　　）

  A．?

  B．{1}

  C．{-1，0，1}

  D．{-1，0，1，2}
  組卷：59引用：1難度：0.8

  解析

• 2．已知命題p：?x∈R，x²-x+1＜0，那么命題p的否定是（　　）

  A．?x∈R，x2-x+1＜0	B．?x∈R，x2-x+1≥0
  C．?x∈R，x2-x+1≥0	D．?x∈R，x2-x+1＜0
  組卷：111引用：7難度：0.8

  解析

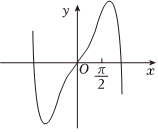• 3．已知函數f（x）的部分圖象如圖，則函數f（x）的解析式可能為（　　）

  A．f（x）=（2x+2-x）sinx	B．f（x）=（2x-2-x）sinx
  C．f（x）=（2x+2-x）cosx	D．f（x）=（2x-2-x）cosx
  組卷：78引用：2難度：0.7

  解析

• 4．“x²＜x”的充要條件的是（　　）

  A．x＜1

  B． 1 x ＞ 1

  C．|x2-x|=x-x2

  D． 3 x 2 ＞ 3 x
  組卷：58引用：1難度：0.8

  解析

• 5．已知a=0.9^1.3，b=1.3^0.9，c=log₂3，則（　　）

  A．a＜c＜b

  B．c＜a＜b

  C．a＜b＜c

  D．c＜b＜a
  組卷：809引用：9難度：0.8

  解析

• 6．已知函數

  f

  （

  x

  ）

  =

  2

  cos

  （

  2

  x

  -

  π

  3

  ）

  （

  x

  ∈

  [

  0

  ，

  π

  ]

  ）

  ，且

  f

  （

  x

  1

  ）

  =

  f

  （

  x

  2

  ）

  =

  4

  5

  （

  x

  1

  ≠

  x

  2

  ）

  ，則x₁+x₂=（　　）

  A． 5 π 6

  B． 4 π 3

  C． 5 π 3

  D． 2 π 3
  組卷：176引用：4難度：0.8

  解析

三、解答題：本大題共5題，共75分。解答應寫出文字說明，證明過程或演算步驟。

• 19．設函數

  f

  （

  x

  ）

  =

  a

  2

  x

  -

  b

  a

  x

  （

  a

  ＞

  0

  ，

  且

  a

  ≠

  1

  ）

  是定義域為R的奇函數，且y=f（x）的圖象過點

  （

  1

  ，

  3

  2

  ）

  ．
  （Ⅰ）求a,b的值；
  （Ⅱ）設g（x）=（x-p）（x-q）²，p＜q,若?x∈R，f（-g（x））+f（mxg'（x））≤0（g'（x）為函數g（x）的導數），試寫出符合上述條件的函數g（x）的一個解析式，并說明你的理由．
  組卷：23引用：1難度：0.4

  解析

• 20．已知函數f（x）=axlnx+x²，a∈R．
  （Ⅰ）若曲線y=f（x）在x=1處的切線斜率為1，求a的值；
  （Ⅱ）討論f（x）的零點個數；
  （Ⅲ）若x∈（1，+∞）時，不等式

  f

  （

  x

  ）

  +

  x

  e

  x

  ＞

  x

  a

  +

  1

  恒成立，求a的最小值．
  組卷：141引用：1難度：0.2

  解析