2022年湖南師大附中高考數學模擬試卷（三）（三模）

一、選擇題：本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．已知集合A={1，2，3}，B={x|x²-6x+m=0}，若A∩B={2}，則B=（　　）

  A．{2，8}

  B．{2，4}

  C．{2，3}

  D．{2，1}
  組卷：146引用：3難度：0.8

  解析

• 2．若

  x

  6

  =

  a

  0

  +

  a

  1

  （

  x

  -

  1

  ）

  +

  a

  2

  （

  x

  -

  1

  ）

  2

  +

  ?

  +

  a

  6

  （

  x

  -

  1

  ）

  6

  ，則a₄=（　　）

  A．1

  B．6

  C．15

  D．20
  組卷：204引用：3難度：0.8

  解析

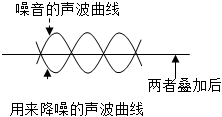• 3．某智能主動降噪耳機工作的原理是利用芯片生成與噪音的相位相反的聲波，通過兩者疊加完全抵消掉噪音（如圖）．已知噪音的聲波曲線y=Asin（ax+p）（其中A＞0，a＞0，0≤φ＜2π）的振幅為1，周期為π，初相為

  π

  2

  ，則用來降噪的聲波曲線的解析式為（　　）

  A．y=sin2x

  B．y=cos2x

  C．y=-sin2x

  D．y=-cos2x
  組卷：103引用：4難度：0.8

  解析

• 4．藝術家們常用正多邊形來設計漂亮的圖案，我國國旗上五顆耀眼的正五角星就是源于正五邊形，正五角星是將正五邊形的任意兩個不相鄰的頂點用線段連接，并去掉正五邊形的邊后得到的圖形，它的中心就是這個正五邊形的中心．如圖，設O是正五角形ABCDE的中心，則下列關系錯誤的是（　　）

  A． AD + DB = OB - OA	B． AO ? BE = 0
  C． AC + AD = 3 AO	D． AO ? AD = BO ? BD
  組卷：116引用：2難度：0.5

  解析

• 5．某型號的燈泡使用壽命為一年以上的概率為p₁，使用壽命兩年以上的概率為p₂.若一只該型號的燈泡已經安全使用了一年，則能再安全使用一年的概率為（　　）

  A．p1-p2

  B．p1?p2

  C． p 1 p 2

  D． p 2 p 1
  組卷：131引用：2難度：0.9

  解析

• 6．下列兩數的大小關系中正確的是（　　）

  A．π3＞3π

  B． 3 3 ＞ 4 4

  C．2ln3＜3ln2

  D．tan1＜1
  組卷：112引用：2難度：0.7

  解析

• 7．已知雙曲線C：x²-3y²=1的左，右頂點分別為A、B，P是C在第一象限的圖象上的點，記∠PAB=α，∠PBA=β，∠APB=γ，則（　　）

  A．tanα+tanβ+tanγ=0	B．tanα+tanβ-tanγ=0
  C．3tanα+3tanβ+4tanγ=0	D．2tanα+2tanβ+3tanγ=0
  組卷：111引用：1難度：0.6

  解析

四、解答題：本題共6小題，共70分.解答應寫出文字說明、證明過程或演算步驟.

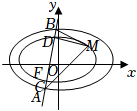• 21．若橢圓

  C

  1

  ：

  x

  2

  a

  2

  1

  +

  y

  2

  b

  2

  1

  =

  1

  與橢圓

  C

  2

  ：

  x

  2

  a

  2

  2

  +

  y

  2

  b

  2

  2

  =

  1

  滿足

  a

  1

  a

  2

  =

  b

  1

  b

  2

  =

  m

  （

  m

  ＞

  0

  ）

  ，則稱這兩個橢圓為“相似”，相似比為m.如圖，已知橢圓C₁的長軸長是4，橢圓C₂的離心率為

  2

  2

  ，橢圓C₁與橢圓C₂相似比為

  2

  ．
  （1）求橢圓C₁與橢圓C₂的方程；
  （2）過橢圓C₂左焦點F的直線l與C₁、C₂依次交于A、C、D、B四點．
  ①求證：無論直線l的傾斜角如何變化，恒有|AC|=|DB|．
  ②點M是橢圓C₂上異于C、D的任意一點，記△MBD面積為S₁，△MAD面積為S₂，當

  S

  1

  =

  1

  5

  S

  2

  時，求直線l的方程．
  組卷：177引用：1難度：0.3

  解析

• 22．已知函數

  f

  （

  x

  ）

  =

  1

  2

  a

  x

  2

  +

  x

  -

  e

  x

  ．
  （1）若a=1，求不等式f（lnx）＞-1的解集；
  （2）當a＞1時，求證函數f（x）在（0，+∞）上存在極值點m,且

  f

  （

  m

  ）

  ＞

  m

  -

  3

  2

  ．
  組卷：158引用：3難度：0.5

  解析