2013-2014學(xué)年江蘇省揚(yáng)州市高郵市臨澤初中九年級（上）國慶數(shù)學(xué)作業(yè)

一．選擇題（每小題3分，共24分．）

• 1．已知等腰三角形的一個(gè)內(nèi)角為40°，則這個(gè)等腰三角形的頂角為（　　）

  A．40°

  B．100°

  C．40°或100°

  D．70°或50°
  組卷：874引用：84難度：0.9

  解析

• 2．正方形具備而菱形不具備的性質(zhì)是（　　）

  A．對角線互相平分

  B．對角線互相垂直

  C．對角線相等

  D．每條對角線平分一組對角
  組卷：367引用：42難度：0.9

  解析

• 3．如圖，已知四邊形ABCD是平行四邊形，下列結(jié)論中不正確的是（　　）

  A．當(dāng)AB=BC時(shí)，它是菱形

  B．當(dāng)AC⊥BD時(shí)，它是菱形

  C．當(dāng)∠ABC=90°時(shí)，它是矩形

  D．當(dāng)AC=BD時(shí)，它是正方形
  組卷：4625引用：291難度：0.9

  解析

• 4．若一組數(shù)據(jù)1，2，3，x的極差為6，則x的值是（　　）

  A．7

  B．8

  C．9

  D．7或-3
  組卷：206引用：68難度：0.9

  解析

• 5．樣本方差的計(jì)算式S²=

  1

  90

  [（x₁-30）²+（x₂-30）²+…+（x_n-30）²]中，數(shù)字90和30分別表示樣本中的（　　）

  A．眾數(shù)、中位數(shù)

  B．方差、標(biāo)準(zhǔn)差

  C．樣本中數(shù)據(jù)的個(gè)數(shù)、平均數(shù)

  D．樣本中數(shù)據(jù)的個(gè)數(shù)、中位數(shù)
  組卷：64引用：27難度：0.9

  解析

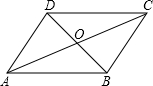• 6．如圖所示，平行四邊形ABCD中，對角線AC和BD相交于點(diǎn)O，如果AC=12，BD=10，AB=m,則m的取值范圍是（　　）

  A．10＜m＜12

  B．2＜m＜22

  C．1＜m＜11

  D．5＜m＜6
  組卷：1325引用：80難度：0.9

  解析

• 7．下列說法：①一組對邊平行，另一組對邊相等的四邊形是平行四邊形或等腰梯形． ②一組對邊平行，一組對角相等的四邊形是平行四邊形．③兩組對角分別相等的四邊形是平行四邊形．④順次連接等腰梯形各邊中點(diǎn)所得到的四邊形是菱形．其中正確的是（　　）

  A．①②

  B．①②③

  C．②③④

  D．①②③④
  組卷：153引用：4難度：0.9

  解析

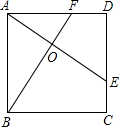• 8．如圖所示，E、F分別是正方形ABCD的邊CD，AD上的點(diǎn)，且CE=DF，AE，BF相交于點(diǎn)O，下列結(jié)論①AE=BF；②AE⊥BF；③AO=OE；④S_△AOB=S_{四邊形DEOF}中，錯(cuò)誤的有（　　）

  A．1個(gè)

  B．2個(gè)

  C．3個(gè)

  D．4個(gè)
  組卷：2176引用：100難度：0.9

  解析

三．解答題：（86分）

• 25．一次期中考試中，甲、乙、丙、丁、戊五位同學(xué)的數(shù)學(xué)、英語成績等有關(guān)信息如下表所示：（單位：分）
  

  	甲	乙	丙	丁	戊	平均分	標(biāo)準(zhǔn)差
  數(shù)學(xué)	71	72	69	68	70		2
  英語	88	82	94	85	76	85

  （1）求這五位同學(xué)在本次考試中數(shù)學(xué)成績的平均分和英語成績的標(biāo)準(zhǔn)差；
  （2）為了比較不同學(xué)科考試成績的好與差，采用標(biāo)準(zhǔn)分是一個(gè)合理的選擇，標(biāo)準(zhǔn)分的計(jì)算公式：
  標(biāo)準(zhǔn)分=（個(gè)人成績一平均成績）÷成績標(biāo)準(zhǔn)差．
  從標(biāo)準(zhǔn)分看，標(biāo)準(zhǔn)分大的考試成績更好，請問甲同學(xué)在本次考試中，數(shù)學(xué)與英語哪個(gè)學(xué)科考得更好？
  組卷：394引用：44難度：0.1

  解析

• 26．如圖1，四邊形ABCD是正方形，G是CD邊上的一個(gè)動(dòng)點(diǎn)（點(diǎn)G與C、D不重合），以CG為一邊在正方形ABCD外作正方形CEFG，連接BG，DE．我們探究下列圖中線段BG、線段DE的長度關(guān)系及所在直線的位置關(guān)系：
  （1）①猜想如圖1中線段BG、線段DE的長度關(guān)系及所在直線的位置關(guān)系；
  ②將圖1中的正方形CEFG繞著點(diǎn)C按順時(shí)針（或逆時(shí)針）方向旋轉(zhuǎn)任意角度α，得到如圖2，如圖3情形．請你通過觀察、測量等方法判斷①中得到的結(jié)論是否仍然成立，并選取圖2證明你的判斷；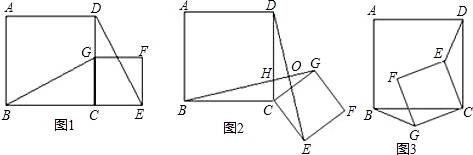
  
  （2）將原題中正方形改為矩形（如圖4-6），且AB=a,BC=b,CE=ka,CG=kb（a≠b,k＞0），第（1）題①中得到的結(jié)論哪些成立，哪些不成立？若成立，以圖5為例簡要說明理由；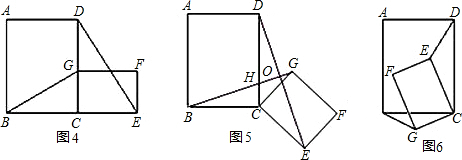
  
  （3）在第（2）題圖5中，連接DG、BE，且a=3，b=2，k=

  1

  2

  ，求BE²+DG²的值．
  組卷：1668引用：42難度：0.1

  解析