當前位置：試卷中心 > 試卷詳情

2023-2024學年黑龍江省哈爾濱十三中高三（上）期中數學試卷

發布：2024/10/23 13:0:1

1．已知集合A={x||x-2|＜1}，B={x|log₂x＜1}，則A∪B=（　　）
A．（0，3） B．（1，2） C．（-∞，3） D．（0，2）
組卷：24引用：3難度：0.9
解析
2．若復數z滿足zi=2-i（i為虛數單位），則z在復平面上所對應的點位于（　　）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
組卷：92引用：5難度：0.8
解析
3．在正項等比數列{a_n}中，a₂+a₆=10，a₄=4，則{a_n}的公比q=（　　）
A．2 B．
2
C．2或
1
2
D．
2
或
2
2
組卷：269引用：2難度：0.7
解析
4．已知圓臺上下底面半徑之比為1：2，母線與底面所成的角的正弦值為
3
5
，圓臺體積為14π，則該圓臺的側面面積為（　　）
A．30π B．18π C．15π D．9π
組卷：110引用：3難度：0.8
解析
5．小明同學為了估算位于哈爾濱的索菲亞教堂的高度，在索菲亞教堂的正東方向找到一座建筑物AB，高為
10
（
3
-
3
）
m
，在它們之間的地面上的點M（B，M，D三點共線）處測得樓頂A，教堂頂C的仰角分別是15°和60°，在樓頂A處測得塔頂C的仰角為30°，則小明估算索菲亞教堂的高度為（　　）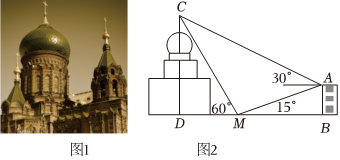
A．60m B．
30
3
m
C．
20
3
m
D．30m
組卷：33引用：1難度：0.6
解析
6．在△ABC中，已知向量
AB
=
（
cos
18
°
，
cos
72
°
）
，
AC
=
（
2
cos
63
°
，
2
cos
27
°
）
，則cos∠BAC的值為（　　）
A．0 B．
1
2
C．
2
2
D．
3
2
組卷：92引用：8難度：0.9
解析
7．若函數
f
（
x
）
=
sin
（
ωx
+
π
6
）
（
ω
＞
0
）
在區間（0，π）上既有最大值，又有最小值，則ω的取值范圍為（　　）
A．
（
4
3
，
+
∞
）
B．
[
4
3
，
+
∞
）
C．（2，+∞） D．[2，+∞）
組卷：131引用：4難度：0.6
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題

21．已知函數f（x）=
m
x
+lnx,m∈R．
（1）討論f（x）的單調性；
（2）證明：當m＞0時，mf（x）≥2m-1．
組卷：113引用：6難度：0.5
解析
22．已知數列{a_n}的首項為1，設
f
（
n
）
=
a
1
C
1
n
+
a
2
C
2
n
+
…
+
a
k
C
k
n
+
?
s
+
a
n
C
n
n
，n∈N^*．
（1）若{a_n}為常數列，求f（8）的值；
（2）若{a_n}為公比為2的等比數列，求f（n）的解析式；
（3）數列{a_n}能否成等差數列，使得f（n）-1=2ⁿ?（n-1）對一切n∈N^*都成立？若能，求出數列的通項公式，若不能，試說明理由．
組卷：63引用：3難度：0.5
解析