2022年廣東省深圳市光明高級(jí)中學(xué)高考數(shù)學(xué)模擬試卷

一、單項(xiàng)選擇題：本題共8小題，每小題5分，共40分．在每小題給出的四個(gè)選項(xiàng)中，只有一個(gè)選項(xiàng)是符合題目要求的．

• 1．設(shè)全集U=R，集合A={x|x²-3x≤0}，B={y|y=2^x}，則A∩（?_UB）=（　　）

  A．（0，3]

  B．{0}

  C．（-∞，0]

  D．[-3，1]
  組卷：137引用：1難度：0.8

  解析

• 2．已知復(fù)數(shù)z在復(fù)平面內(nèi)對(duì)應(yīng)點(diǎn)的坐標(biāo)為（3，-4），則

  z

  4

  +

  3

  i

  =（　　）

  A．-i

  B．i

  C．3-4i

  D．5
  組卷：96引用：1難度：0.8

  解析

• 3．已知角θ的終邊與單位圓的交點(diǎn)在直線

  x

  +

  y

  =

  13

  13

  上，則sin2θ=（　　）

  A． - 12 13

  B． - 13 13

  C． 1 13

  D． 12 13
  組卷：124引用：1難度：0.7

  解析

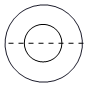• 4．通用技術(shù)老師指導(dǎo)學(xué)生制作統(tǒng)一規(guī)格的圓臺(tái)形容器，用如圖所示的圓環(huán)沿虛線剪開(kāi)得到的一個(gè)半圓環(huán)（其中小圓和大圓的半徑分別是1cm和4cm）制作該容器的側(cè)面，則該圓臺(tái)形容器的高為（　　）

  A． 3 2 cm

  B．1cm

  C． 3 cm

  D． 3 3 2 cm
  組卷：79引用：1難度：0.6

  解析

• 5．若函數(shù)f（x）=|tan（ωx-ω）|（ω＞0）的最小正周期為4，則下列區(qū)間中f（x）單調(diào)遞增的是（　　）

  A． （ - 1 ， 1 3 ）

  B． （ 1 3 ， 5 3 ）

  C． （ 5 3 ， 3 ）

  D．（3，4）
  組卷：194引用：2難度：0.7

  解析

• 6．已知函數(shù)f（x）=x³+ax²-x+a有兩個(gè)極值點(diǎn)x₁，x₂，且

  |

  x

  1

  -

  x

  2

  |

  =

  2

  3

  3

  ，則f（x）的極大值為（　　）

  A． 3 9

  B． 2 3 9

  C． 3 3

  D． 3
  組卷：237引用：8難度：0.6

  解析

• 7．已知數(shù)列{a_n}中，a₁=1，a₂=2，

  a

  n

  +

  2

  =

  （

  -

  1

  ）

  n

  +

  1

  a

  n

  +

  2

  ，則

  a

  18

  a

  19

  =（　　）

  A．3

  B． 1 13

  C． 2 13

  D． 2 19
  組卷：241引用：1難度：0.7

  解析

四、解答題：本題共6小題，共70分．解答應(yīng)寫(xiě)出文字說(shuō)明、證明過(guò)程或演算步驟．

• 21．已知函數(shù)f（x）=

  ax

  e

  x

  （a≠0）．
  （1）若對(duì)任意的x∈R，都有

  f

  （

  x

  ）

  ≤

  1

  e

  恒成立，求實(shí)數(shù)a的取值范圍；
  （2）設(shè)m,n是兩個(gè)不相等的實(shí)數(shù)，且m=ne^m-n．求證：m+n＞2．
  組卷：189引用：1難度：0.3

  解析

• 22．已知直線l：x-2y+5=0與橢圓

  C

  ：

  x

  2

  4

  +

  y

  2

  =

  1

  ．過(guò)直線l上一點(diǎn)P（x₀，y₀）作橢圓C的兩條切線，切點(diǎn)分別為A，B．
  （1）求證：直線AB恒過(guò)定點(diǎn)；
  （2）設(shè)O為坐標(biāo)原點(diǎn)，當(dāng)點(diǎn)P不在坐標(biāo)軸上且

  OA

  ?

  OB

  =

  0

  時(shí)，求此時(shí)點(diǎn)P的坐標(biāo)．
  組卷：249引用：1難度：0.3

  解析