2018年第二十三屆“華羅庚金杯”少年數學邀請賽決賽試卷（小高組）
發布：2024/4/20 14:35:0
一、填空題（共8小題，每小題10分，滿分80分）
-
1．如圖，一個4×4方形點陣，每個點與其相鄰的上、下、左、右點的距離都相等．以這些點為端點的、不同長度的線段共有條．組卷：16引用：1難度：0.8 -
2．a,b,c,d四個數，每次去掉2個數，將其余2個數求平均數，這樣計算了6次，得到6個數是：23，26，29，32，24，31，則四個數a,b,c,d的平均數是．
組卷：215引用：1難度：0.6 -
3．甲、乙兩車從同一地點出發沿同一高速公路從A地到B地．甲車先出發2小時，乙車出發后經5小時與甲車同時到達B地．如果乙車時速增加8千米，那么，出發后4小時可追上甲車．A地與B地的距離是千米．
組卷：245引用：1難度：0.4 -
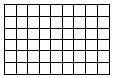4．如圖，一個6×9方格網．先將其中的任意幾個方格染黑，然后按照以下規則繼續染色：如果某個方格至少與2個黑格都有公共邊，那么就將這個方格染黑．要按照這個規則將整個棋盤都染成黑色，所需要的最少初始染黑方格是個．組卷：31引用：2難度：0.2
三、解答下列各題（每小題15分，共30分，要求寫出詳細過程）
-
13．記1×2×3×4×……×2018=12m×A×10n，其中A是使得式子成立的最小的整數，那么m,n的值分別是多少？A是否被2和3整除？
組卷：55引用：1難度：0.5 -
14．任意寫下k個不同的二位數，其中必有3個構成某個三角形的三條邊的長度，求k的最小值．
組卷：63引用：2難度：0.3