2022年湖南省長沙一中高考數學一模試卷

一、選擇題：本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一個選項是符合題目要求的．

• 1．設集合A，B滿足A∪B={1，2，3，4，5，6}，A∩B={2，4}，A={2，3，4，5}，則B=（　　）

  A．{2，4，5，6}

  B．{1，2，4，6}

  C．{2，4，6}

  D．{1，2，4}
  組卷：169引用：8難度：0.8

  解析

• 2．已知a,b是兩條不同的直線，α，β是兩個不同的平面，且a⊥α，α⊥β，則“a⊥b”是“b⊥β”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充分必要條件	D．既不充分又不必要條件
  組卷：243引用：4難度：0.7

  解析

• 3．某地區經過一年的新農村建設，農村的經濟收入增加了一倍，實現翻番．為更好地了解該地區農村的經濟收入變化情況、統計了該地區新農村建設前后農村的經濟收入構成比例；得到如下餅圖：
  
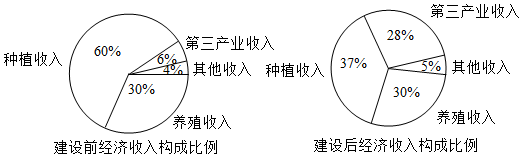
  則下面結論中不正確的是（　　）

  A．新農村建設后，種植收入減少

  B．新農村建設后，其他收入增加了一倍以上

  C．新農村建設后，養殖收入增加了一倍

  D．新農村建設后，養殖收入與第三產業收入的總和超過了經濟收入的一半
  組卷：94引用：21難度：0.7

  解析

• 4．《九章算術》是我國古代的一本數學名著．全書為方田、粟米、衰分、少廣、商功、均輸、盈不足、方程、勾股九章，收有246個與生產、生活實踐有聯系的應用問題．在第六章“均輸”中有這樣一道題目：“今有五人分五錢，令上二人所得與下三人等，問各得幾何？”其意思為：“現有五個人分5錢，每人所得成等差數列，且較多的兩份之和等于較少的三份之和，問五人各得多少？”在此題中，任意兩人所得的最大差值為多少？（　　）

  A． 1 3

  B． 2 3

  C． 1 6

  D． 5 6
  組卷：352引用：11難度：0.7

  解析

• 5．已知

  sin

  （

  θ

  -

  π

  4

  ）

  =

  2

  2

  3

  ，則sin2θ的值為（　　）

  A． 7 9

  B． - 7 9

  C． 2 9

  D． - 2 9
  組卷：282引用：5難度：0.7

  解析

• 6．若函數f（x+1）為偶函數，對任意x₁，x₂∈[1，+∞）且x₁≠x₂，都有（x₂-x₁）[f（x₁）-f（x₂）]＞0，則有（　　）

  A． f （ 1 3 ） ＜ f （ 3 2 ） ＜ f （ 2 3 ）	B． f （ 2 3 ） ＜ f （ 3 2 ） ＜ f （ 1 3 ）
  C． f （ 2 3 ） ＜ f （ 1 3 ） ＜ f （ 3 2 ）	D． f （ 3 2 ） ＜ f （ 2 3 ） ＜ f （ 1 3 ）
  組卷：911引用：5難度：0.7

  解析

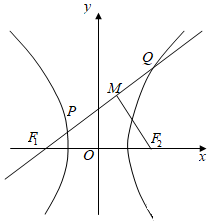• 7．如圖，F₁，F₂是雙曲線l：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =1（a＞0，b＞0）的左、右焦點，過F₁的直線與雙曲線左、右兩支分別交于點P，Q．若

  F

  1

  Q

  =5

  F

  1

  P

  ，M為PQ的中點，且

  F

  1

  Q

  ⊥

  F

  2

  M

  ，則雙曲線的離心率為（　　）

  A． 14 2

  B． 7 2

  C． 2

  D．2
  組卷：428引用：7難度：0.7

  解析

四、解答題：本題共6小題，共70分．解答應寫出文字說明，證明過程或演算步驟．

• 21．已知橢圓C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  的離心率為

  3

  2

  ，左、右焦點分別為F₁，F₂，A為C的上頂點，且△AF₁F₂的周長為

  4

  +

  2

  3

  ．
  （1）求橢圓C的方程；
  （2）直線l：y=kx+m（m≠0）與橢圓C交于M，N兩點，O為坐標原點，當k為何值，|OM|²+|ON|²恒為定值，并求此時△MON面積的最大值．
  組卷：313引用：4難度：0.5

  解析

• 22．已知函數f（x）=（x+b）（e^x-a）（b＞0）在（-1，f（-1））處的切線l方程為（e-1）x+ey+e-1=0．
  （1）求a,b,并證明函數y=f（x）的圖象總在切線l的上方（除切點外）；
  （2）若方程f（x）=m有兩個實數根x₁，x₂，且x₁＜x₂，證明：

  x

  1

  -

  x

  2

  ≤

  1

  +

  m

  （

  1

  -

  2

  e

  ）

  1

  -

  e

  ．
  組卷：176引用：1難度：0.3

  解析