2022-2023學年江西省南昌市高一（上）期中數學試卷

一、選擇題：本題共8小題，每小題5分，共40分。在每小題給出的四個選項中，只有一項是符合題目要求的。

• 1．已知集合A={1，2，3}，B={x|x（2-x）≤0}，則A∩B=（　　）

  A．{2，3}

  B．{1，3}

  C．{1，2}

  D．{1，2，3}
  組卷：59引用：2難度：0.8

  解析

• 2．命題“存在兩個不同的無理數a,b,使得a+b是無理數”的否定為（　　）

  A．存在兩個相同的無理數a,b,使得a+b是有理數

  B．存在兩個相同的有理數a,b,使得a+b是有理數

  C．任意兩個不同的無理數a,b,都有a+b是無理數

  D．任意兩個不同的無理數a,b,都有a+b是有理數
  組卷：25引用：1難度：0.8

  解析

• 3．若函數f（x）=x³+ax²為奇函數，則實數a=（　　）

  A．0

  B．-1

  C．1

  D．±1
  組卷：223引用：2難度：0.9

  解析

• 4．1∈[m,+∞）成立的一個必要不充分條件是（　　）

  A．m=1

  B．m≤1

  C．m=2

  D．m≤2
  組卷：31引用：1難度：0.7

  解析

• 5．已知a=（2

  2

  ）²，b=4

  2

  ，c=2^π，則a,b,c的大小關系為（　　）

  A．a＜b＜c

  B．b＜a＜c

  C．b＜c＜a

  D．c＜b＜a
  組卷：66引用：1難度：0.8

  解析

• 6．網貸因高利息和多套路，令人深惡痛絕．某平臺的還款金額y（單位：元）與貸款時長x（單位：月）滿足的函
  數關系式為y=a（1+p）^x，某人在該平臺貸款若干，若貸款2個月需還1200元，貸款5個月需還1500元，則貸款11個月大約需還（　　）

  A．2078元

  B．2100元

  C．2344元

  D．2432元
  組卷：46引用：1難度：0.6

  解析

• 7．函數f（x）=

  x

  2

  +

  1

  3

  x

  -

  3

  -

  x

  的大致圖象為（　　）

  A．

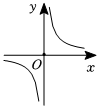
  B．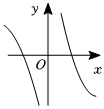

  C．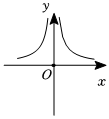

  D．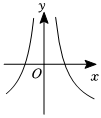
  組卷：148引用：2難度：0.8

  解析

四、解答題：本題共6小題，共70分。解答應寫出文字說明、證明過程或演算步驟。

• 21．已知函數f（x）=a^x+b,f（1）=1．
  （1）若a＞0，b＞0，求

  1

  a

  2

  +

  ab

  +

  4

  b

  的最小值；
  （2）若對任意的x,y都有f（x+y）=f（x）f（y）+f（x）+f（y），設F（x）=x（

  1

  2

  -

  1

  f

  （

  x

  ）

  +

  2

  ），求證：F（x）為偶函數．
  組卷：51引用：1難度：0.7

  解析

• 22．已知定義在R上的偶函數g（x）和奇函數h（x），滿足g（x）+h（x）=2^x．
  （1）求

  h

  （

  x

  ）

  g

  （

  x

  ）

  的值域；
  （2）記f（x）=

  h

  （

  x

  ）

  g

  （

  x

  ）

  +

  2

  ，求證：對任意的實數x₁，x₂，均存在以f（x₁），f（x₂），f（0）為三邊邊長的三角形．
  組卷：28引用：1難度：0.7

  解析