2023-2024學(xué)年陜西省、青海省四川省名校聯(lián)盟高三（上）第二次月考數(shù)學(xué)試卷（文科）（01）

一、選擇題：本題共12小題，每小題5分，共60分。在每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)是符合題目要求的。

• 1．設(shè)集合S={x|x＜-1或x＞5}，T={x|a＜x＜a+8}，S∪T=R，則實(shí)數(shù)a的取值范圍是（　　）

  A．（-3，-1）	B．[-3，-1]
  C．（-∞，-3）∪[-1，+∞）	D．（-∞，-3）∪（-1，+∞）
  組卷：158引用：4難度：0.8

  解析

• 2．命題“?n∈N*，?x∈R，使得n²＜x”的否定形式是（　　）

  A．?n∈N*，?x∈R，使得n2≥x	B．?n∈N*，?x∈R，使n2≥x
  C．?n∈N*，?x∈R，使得n2≥x	D．?n∈N*，?x∈R，使得n2≥x
  組卷：110引用：8難度：0.9

  解析

• 3．點(diǎn)P從（1，0）出發(fā)，沿單位圓逆時(shí)針?lè)较蜻\(yùn)動(dòng)

  4

  π

  3

  弧長(zhǎng)到達(dá)Q點(diǎn)，則Q點(diǎn)的坐標(biāo)為（　　）

  A． （ - 1 2 ， 3 2 ）

  B． （ - 3 2 ，- 1 2 ）

  C． （ - 1 2 ，- 3 2 ）

  D． （ - 3 2 ， 1 2 ）
  組卷：292引用：8難度：0.9

  解析

• 4．函數(shù)y=

  sin

  2

  x

  1

  +

  cosx

  的部分圖象大致為（　　）

  A．

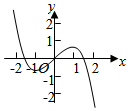
  B．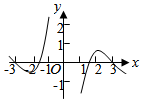

  C．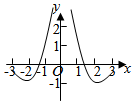

  D．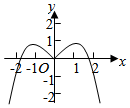
  組卷：119引用：8難度：0.7

  解析

• 5．科學(xué)家康斯坦丁?齊奧爾科夫斯基在1903年提出單級(jí)火箭在不考慮空氣阻力和地球引力的理想情況下的最大v滿足公式：

  v

  =

  v

  0

  ln

  m

  1

  +

  m

  2

  m

  1

  ，其中m₁，m₂分別為火箭結(jié)構(gòu)質(zhì)量和推進(jìn)劑的質(zhì)量，v₀是發(fā)動(dòng)機(jī)的噴氣速度．已知某實(shí)驗(yàn)用的單級(jí)火箭模型結(jié)構(gòu)質(zhì)量為akg,若添加推進(jìn)劑3akg,火箭的最大速度為2.8km/s,若添加推進(jìn)劑5akg,則火箭的最大速度約為（　　）（參考數(shù)據(jù)：ln2≈0.7，ln3≈1.1）

  A．4.7km/s

  B．4.2km/s

  C．3.6km/s

  D．3.1km/s
  組卷：193引用：6難度：0.6

  解析

• 6．已知函數(shù)f（x）=ax³+bx+1的圖象在點(diǎn)（1，a+b+1）處的切線斜率為6，且函數(shù)f（x）在x=2處取得極值，則a+b=（　　）

  A． - 26 3

  B．7

  C． 22 3

  D． 26 3
  組卷：630引用：7難度：0.7

  解析

• 7．在△ABC中，內(nèi)角A、B、C所對(duì)的邊分別為a、b、c,若

  sin

  （

  3

  2

  B

  +

  π

  4

  ）

  =

  2

  2

  ，且a+c=2，則△ABC周長(zhǎng)的取值范圍是（　　）

  A．（2，3]

  B．[3，4）

  C．（4，5]

  D．[5，6）
  組卷：45引用：3難度：0.7

  解析

三、解答題：本題共6小題，共70分。解答應(yīng)寫出文字說(shuō)明、證明過(guò)程或演算步驟。

• 21．已知函數(shù)f（x）=-e^-x-cx（c∈R）．
  （1）若c≤0，函數(shù)f（x）在區(qū)間[-1，2]上的最小值為-1-e,求c的值；
  （2）設(shè)g（x）=f（x）+e^x，若函數(shù)g（x）有極值，求實(shí)數(shù)c的取值范圍．
  組卷：54引用：3難度：0.6

  解析

• 22．已知函數(shù)f（x）=lnx-ax-1（a＞0）．
  （1）當(dāng)a=1時(shí)，求過(guò)原點(diǎn)且與f（x）相切的直線方程；
  （2）若g（x）=x+e^ax?f（x）（a＞0）有兩個(gè)不同的零點(diǎn)x₁，x₂（0＜x₁＜x₂），不等式

  x

  1

  ?

  x

  2

  2

  ＞

  e

  m

  恒成立，求實(shí)數(shù)m的取值范圍．
  組卷：172引用：4難度：0.3

  解析