《第2章 圓錐曲線與方程》2010年單元測試卷（1）

一、選擇題（共5小題，每小題3分，滿分15分）

• 1．已知拋物線y²=2px（p＞0）與雙曲線

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  （a,b＞0）有相同的焦點F，點A是兩曲線的一個交點，且AF⊥x軸，若l為雙曲線的一條斜率大于0的漸近線，則l的斜率可以在下列給出的某個區間內，該區間可以是（　　）

  A． （ 0 ， 3 3 ）

  B． （ 3 3 ， 1 ）

  C． （ 1 ， 2 ）

  D． （ 2 ， + ∞ ）
  組卷：128引用：8難度：0.7

  解析

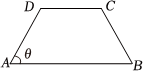• 2．如圖，在等腰梯形ABCD中，AB∥CD，且AB=2AD，設∠DAB=θ，θ∈（0，

  π

  2

  ），以A，B為焦點且過點D的雙曲線的離心率為e₁，以C，D為焦點且過點A的橢圓的離心率為e₂，則（　　）

  A．隨著角度θ的增大，e1增大，e1e2為定值

  B．隨著角度θ的增大，e1減小，e1e2為定值

  C．隨著角度θ的增大，e1增大，e1e2也增大

  D．隨著角度θ的增大，e1減小，e1e2也減小
  組卷：1293引用：38難度：0.9

  解析

• 3．已知橢圓

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞0，b＞0），A是橢圓長軸的一個端點，B是橢圓短軸的一個端點，F為橢圓的一個焦點．若AB⊥BF，則該橢圓的離心率為（　　）

  A． 5 + 1 2

  B． 5 - 1 2

  C． 5 + 1 4

  D． 5 - 1 4
  組卷：184引用：6難度：0.7

  解析

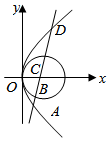• 4．如圖拋物線C₁：y²=2px和圓C₂：

  （

  x

  -

  p

  2

  ）

  2

  +y²=

  p

  2

  4

  ，其中p＞0，直線l經過C₁的焦點，依次交C₁，C₂于A，B，C，D四點，則

  AB

  ?

  CD

  的值為（　　）

  A． p 2 4

  B． p 2 3

  C． p 2 2

  D．p2
  組卷：240引用：7難度：0.9

  解析

• 5．已知點P是拋物線y²=2x上的一個動點，則點P到點（0，2）的距離與P到該拋物線準線的距離之和的最小值為（　　）

  A． 17 2

  B．3

  C． 5

  D． 9 2
  組卷：1228引用：60難度：0.9

  解析

三、解答題（共8小題，滿分107分）

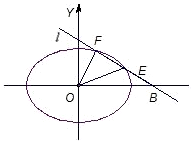• 14．已知橢圓C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  的長軸長為

  2

  2

  ，離心率

  e

  =

  2

  2

  ．
  （1）求橢圓C的標準方程；
  （2）若過點B（2，0）的直線l（斜率不等于零）與橢圓C交于不同的兩點E、F（E在B、F之間），且△OBE與△OBF的面積之比為

  1

  2

  ，求直線l的方程．
  組卷：64引用：10難度：0.5

  解析

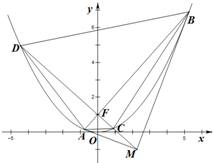• 15．已知拋物線x²=4y的焦點為F，過焦點F且不平行于x軸的動直線l交拋物線于A，B兩點，拋物線在A、B兩點處的切線交于點M．
  （Ⅰ）求證：A，M，B三點的橫坐標成等差數列；
  （Ⅱ）設直線MF交該拋物線于C，D兩點，求四邊形ACBD面積的最小值．
  組卷：73引用：8難度：0.1

  解析