2022-2023學(xué)年湖南省常德市九年級(jí)（上）期末數(shù)學(xué)試卷

一、選擇題（本大題共8小題，每小題3分，共24分）

• 1．一元二次方程5x²-2x+2=0的一次項(xiàng)系數(shù)是（　　）

  A．5

  B．-2

  C．2

  D．0
  組卷：649引用：13難度：0.8

  解析

• 2．已知△ABC的三邊長(zhǎng)分別為4、6、8，與它相似的△DEF的最短邊長(zhǎng)為6，則△DEF的最長(zhǎng)邊的長(zhǎng)為（　　）

  A．8

  B．12

  C．10

  D．9
  組卷：165引用：3難度：0.9

  解析

• 3．在Rt△ABC中，∠C=90°，AB=5，AC=3，則sinB的值為（　　）

  A． 3 4

  B． 4 3

  C． 4 5

  D． 3 5
  組卷：339引用：5難度：0.7

  解析

• 4．已知反比例函數(shù)

  y

  =

  k

  x

  （k＞0）的圖象上有兩點(diǎn)（-2，y₁）（-3，y₂），則y₁與y₂的大小關(guān)系是（　　）

  A．y1＞y2

  B．y1＜y2

  C．y1≥y2

  D．y1≤y2
  組卷：192引用：4難度：0.7

  解析

• 5．對(duì)一組數(shù)據(jù)：5，-5，9，7，9，描述正確的是（　　）

  A．中位數(shù)是9

  B．平均數(shù)是5

  C．眾數(shù)是7

  D．方差是7
  組卷：98引用：3難度：0.7

  解析

• 6．如圖，已知雙曲線

  y

  =

  k

  x

  （

  x

  ＞

  0

  ）

  與矩形OABC的對(duì)角線OB相交于點(diǎn)D，若

  OB

  OD

  =

  5

  3

  ，矩形OABC的面積為

  100

  3

  ，則k等于（　　）

  A．6

  B．12

  C．24

  D．36
  組卷：289引用：2難度：0.7

  解析

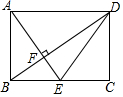• 7．如圖，在矩形ABCD中，點(diǎn)E是邊BC的中點(diǎn)，AE⊥BD，垂足為F，則tan∠BDE的值是（　　）

  A． 2 4

  B． 1 4

  C． 1 3

  D． 2 3
  組卷：4147引用：29難度：0.7

  解析

• 8．二次函數(shù)y=ax²+bx+c（a≠0）的部分圖象如圖所示，對(duì)稱軸為直線

  x

  =

  1

  2

  且經(jīng)過點(diǎn)（2，0）．下列說法：①abc＜0；②-2b+c=0；③4a+2b+c＜0；④若

  （

  -

  1

  2

  ，

  y

  1

  ）

  ，

  （

  5

  2

  ，

  y

  2

  ）

  是拋物線上的兩點(diǎn)，則y₁＜y₂；⑤

  1

  4

  b

  ＞

  m

  （

  am

  +

  b

  ）

  （其中

  m

  ≠

  1

  2

  ）其中正確的結(jié)論有（　　）

  A．2

  B．3

  C．4

  D．5
  組卷：699引用：9難度：0.6

  解析

七、（本大題2個(gè)小題，每小題10分，滿分20分）

• 25．綜合與實(shí)踐
  動(dòng)手操作
  如圖1，在Rt△ABC中，∠C=90°，將△ABC繞點(diǎn)A逆時(shí)針旋轉(zhuǎn)90°得到△AED．延長(zhǎng)ED分別交CB于點(diǎn)F，交AB于點(diǎn)G，連接AF．
  思考探究
  （1）∠CAF=

  °，∠EAG=

  °；
  （2）若BC=（

  2

  +1）AC，則①∠DAG=

  °；②

  FG

  GD

  =

  ，請(qǐng)證明你的結(jié)論；
  開放拓展
  （3）如圖2，若改變旋轉(zhuǎn)角，已知AC=3，BC=4，當(dāng)∠EAF=90°時(shí)，△AFB的面積為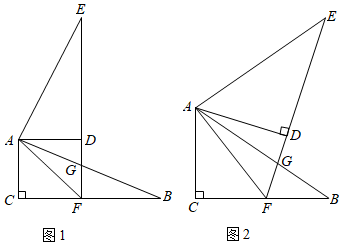

  ．
  組卷：340引用：3難度：0.2

  解析

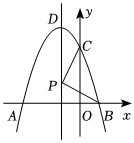• 26．如圖，二次函數(shù)y=ax²-2x+c（a≠0）的圖象交x軸于點(diǎn)A（-3，0），B（1，0），交y軸于點(diǎn)C，頂點(diǎn)為D．
  （1）求二次函數(shù)的解析式；
  （2）點(diǎn)P是拋物線的對(duì)稱軸上一個(gè)動(dòng)點(diǎn)，連接BP，CP，當(dāng)BP+CP的長(zhǎng)度最小時(shí)，求出點(diǎn)P的坐標(biāo)；
  （3）在（2）的條件下，若點(diǎn)E是x軸上一動(dòng)點(diǎn)，在直線BP上是否存在點(diǎn)F，使以B，C，E，F(xiàn)為頂點(diǎn)的四邊形是平行四邊形，若存在，請(qǐng)直接寫出點(diǎn)F的坐標(biāo)；若不存在，請(qǐng)說明理由．
  組卷：655引用：7難度：0.2

  解析