2023-2024學年北京市朝陽區陳經綸中學九年級(上)月考數學試卷(10月份)
發布:2024/9/14 14:0:9
一、選擇題
-
1.在我國古代的房屋建筑中,窗欞是重要的組成部分,具有高度的藝術價值.下列窗欞的圖案中,是中心對稱圖形但不是軸對稱圖形的是( )
A. 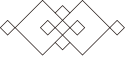
B. 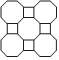
C. 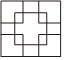
D. 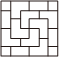 組卷:170引用:8難度:0.9
組卷:170引用:8難度:0.9 -
2.方程x2-x+3=0的根的情況是( )
A.有兩個不相等的實數根 B.有兩個相等的實數根 C.無實數根 D.只有一個實數根 組卷:1134引用:21難度:0.8 -
3.如果點M(-2,y1),N(-1,y2)在二次函數y=-x2+2x的圖象上,那么下列結論正確的是( )
A.y1≤y2 B.y1>y2 C.y1<y2 D.y1≥y2 組卷:8引用:2難度:0.6 -
4.將拋物線y=-(x+1)2向左平移1個單位后,得到的拋物線的頂點坐標是( )
A.(-2,0) B.(0,0) C.(-1,-1) D.(-2,-1) 組卷:133引用:4難度:0.9 -
 5.已知二次函數和一次函數y2=kx+n(k≠0)的圖象如圖所示,下面有四個推斷:y1=ax2+bx+c(a≠0)
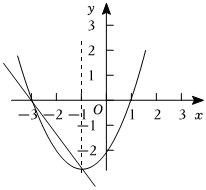
5.已知二次函數和一次函數y2=kx+n(k≠0)的圖象如圖所示,下面有四個推斷:y1=ax2+bx+c(a≠0)
①二次函數y1有最大值;
②當x>-1時,二次函數y1的圖象y隨x的增大而增大;
③當x=-2時,二次函數y1的值大于0;
④過動點P(m,0)且垂直于x軸的直線與y1,y2的圖象的交點分別為C,D,當點C位于點D上方時,m的取值范圍是m<-3或m>-1.
其中正確的是( )A.①③ B.①④ C.②④ D.②③ 組卷:69引用:1難度:0.5 -
6.某型號的手機連續兩次降價,每個售價由原來的1185元降到了580元,設平均每次降價的百分率為x,列出方程正確的是( )
A.580(1+x)2=1185 B.1185(1+x)2=580 C.580(1-x)2=1185 D.1185(1-x)2=580 組卷:947引用:144難度:0.9 -
 7.二次函數y=ax2+bx+c的圖象如圖所示,下列說法正確的個數有( )
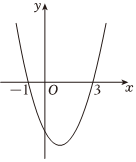
7.二次函數y=ax2+bx+c的圖象如圖所示,下列說法正確的個數有( )
①a+b+c>0;
②ab>0;
③b+2a=0;
④方程ax2+bx+c=5有兩個不相等的實數根.A.1個 B.2個 C.3個 D.4個 組卷:31引用:1難度:0.5 -
 8.如圖,正方形ABCD中,AB=4cm,點E、F同時從C點出發,以1cm/s的速度分別沿CB-BA、CD-DA運動,到點A時停止運動.設運動時間為t(s),△AEF的面積為S(cm2),則S(cm2)與t(s)的函數關系可用圖象表示為( )
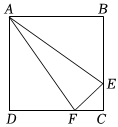
8.如圖,正方形ABCD中,AB=4cm,點E、F同時從C點出發,以1cm/s的速度分別沿CB-BA、CD-DA運動,到點A時停止運動.設運動時間為t(s),△AEF的面積為S(cm2),則S(cm2)與t(s)的函數關系可用圖象表示為( )A. 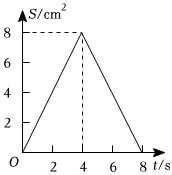
B. 
C. 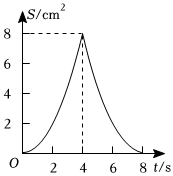
D. 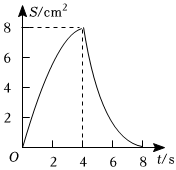 組卷:1495引用:15難度:0.7
組卷:1495引用:15難度:0.7
二、填空題
-
9.在平面直角坐標系中點B的坐標為(3,1),點B關于原點的對稱點的坐標為.
組卷:59引用:7難度:0.9
三、解答題
-
27.小明在學習時遇到這樣一個問題:
如果二次函數y=a1x2+b1x+c1(a1≠0,a1,b1,c1是常數)與y=a2x2+b2x+c2(a2≠0,a2,b2,c2是常數)滿足a1+a2=0,b1=b2,c1+c2=0,則稱這兩個函數互為“旋轉函數”.求y=-x2+3x-2函數的“旋轉函數”.
小明是這樣思考的:由y=-x2+3x-2函數可知a1=-1,b1=3,c1=-2,根據a1+a2=0,b1=b2,c1+c2=0,求出a2,b2,c2,就能確定這個函數的“旋轉函數”.
請參考小明的方法解決下面的問題:
(1)寫出函數y=-x2+3x-2的“旋轉函數”;
(2)若函數y=-x2+mx-2與y=x2-2nx+n互為“旋轉函數”,求(m+n)2016的值;43
(3)已知函數y=-(x+1)(x-4)的圖象與x軸交于A,B兩點,與y軸交于點C,點A,B,C關于原點的對稱點分別是A1,B1,C1,試證明經過點A1,B1,C1的二次函數與函數y=-12(x+1)(x-4)互為“旋轉函數”.12組卷:105引用:2難度:0.3 -
28.正方形ABCD中,將邊AB所在直線繞點A逆時針旋轉一個角度α得到直線AM,過點C作CE⊥AM,垂足為E,連接BE.
(1)當0°<α<45°時,設AM交BC于點F,
①如圖1,若α=35°,則∠BCE=°;
②如圖2,用等式表示線段AE,BE,CE之間的數量關系,并證明;
(2)當45°<α<90°時(如圖3),請直接用等式表示線段AE,BE,CE之間的數量關系.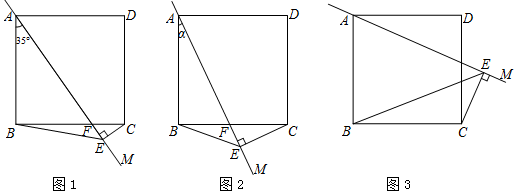 組卷:871引用:7難度:0.4
組卷:871引用:7難度:0.4


