2022-2023學(xué)年新疆實驗中學(xué)高二（上）期中數(shù)學(xué)試卷

一、單選題：本大題共8題，每小題5分，共計40分.在每小題列出的四個選項中只有一項是符合題目要求的.

• 1．若直線l的方向向量

  a

  =

  （

  1

  ，

  2

  ，-

  1

  ）

  ，平面α的一個法向量

  m

  =

  （

  -

  2

  ，-

  4

  ，

  k

  ）

  ，若l⊥α，則實數(shù)k=（　　）

  A．2

  B．-10

  C．-2

  D．10
  組卷：642引用：16難度：0.8

  解析

• 2．圓x²+y²-2x+6y-6=0的圓心和半徑分別是（　　）

  A．（1，-3），16

  B．（-1，-3），16

  C．（1，-3），4

  D．（-1，-3），4
  組卷：164引用：1難度：0.8

  解析

• 3．方程（2x+3y-1）（

  x

  -

  3

  -1）=0表示的曲線是（　　）

  A．兩條直線	B．兩條射線
  C．兩條線段	D．一條直線和一條射線
  組卷：1282引用：17難度：0.7

  解析

• 4．已知直線x-2y+4=0經(jīng)過橢圓

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞b＞0）的頂點和焦點，則橢圓的標準方程為（　　）

  A． x 2 20 + y 2 16 =1	B． x 2 20 + y 2 4 =1
  C． x 2 16 + y 2 12 =1	D． x 2 16 + y 2 4 =1
  組卷：91引用：3難度：0.7

  解析

• 5．已知F₁、F₂為雙曲線C：x²-y²=2的左、右焦點，點P在C上，|PF₁|=2|PF₂|，則cos∠F₁PF₂=（　　）

  A． 1 4

  B． 3 5

  C． 3 4

  D． 4 5
  組卷：2771引用：69難度：0.7

  解析

• 6．在直三棱柱ABC-A₁B₁C₁中，∠BCA=90°，D，F(xiàn)分別是A₁B₁，A₁C₁的中點，BC=CA=CC₁，則BD與AF所成角的正弦值是（　　）

  A． 30 10

  B． 35 10

  C． 70 10

  D． 15 10
  組卷：30引用：1難度：0.6

  解析

• 7．已知點F是拋物線C：y²=4x的焦點，過焦點F的直線l交拋物線C于不同的兩點P，Q，設(shè)

  PF

  =

  3

  FQ

  ，點M為PQ的中點，則M到y(tǒng)軸的距離為（　　）

  A． 4 3

  B． 5 3

  C． 8 3

  D． 7 3
  組卷：179引用：1難度：0.6

  解析

四、解答題：本大題共6題，共計70分.解答應(yīng)寫出文字說明，證明過程或演算步驟.

• 21．在直角梯形CEPD中，PD∥EC，PD=8，CE=6，A為線段PD的中點，四邊形ABCD為正方形．將四邊形PABE沿AB折疊，使得PA⊥AD，得到如圖（2）所示的幾何體．
  （1）求直線PD與平面PCE所成角的正弦值；
  （2）當F為線段AB的中點時，求二面角P-CE-F的余弦值．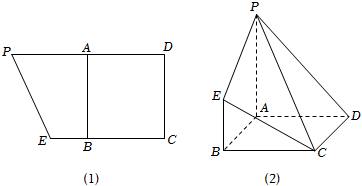
  組卷：68引用：2難度：0.6

  解析

• 22．已知橢圓C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞b＞0），其右焦點為F（

  3

  ，0），點M在圓x²+y²=b²上但不在y軸上，過點M作圓的切線交橢圓于P，Q兩點，當點M在x軸上時，|PQ|=

  3

  ．
  （1）求橢圓C的標準方程；
  （2）當點M在圓上運動時，試探究△FPQ周長的取值范圍．
  組卷：257引用：4難度：0.5

  解析