2023年北京市十一學校中考數學考前適應性試卷(6月份)
發布:2024/7/1 8:0:9
一、選擇題(本題共16分,每題2分)第1-8題均有四個選項,符合題意的選項只有一個
-
 1.如圖是某個幾何體的展開圖,該幾何體是( )
1.如圖是某個幾何體的展開圖,該幾何體是( )A.三棱柱 B.圓錐 C.四棱柱 D.圓柱 組卷:3120引用:45難度:0.9 -
2.芝麻被稱為“八谷之冠”,是世界上最古老的油料作物之一,它作為食品和藥物,得到廣泛的使用.經測算,一粒芝麻的質量約為0.00000201kg,將100粒芝麻的質量用科學記數法表示約為( )
A.20.1×10-3kg B.2.01×10-4kg C.0.201×10-5kg D.2.01×10-6kg 組卷:2678引用:32難度:0.9 -
3.若正多邊形的一個內角是160°,則該多邊形的邊數為( )
A.10 B.12 C.18 D.20 組卷:195引用:1難度:0.7 -
 4.實數a,b,c在數軸上對應點的位置如圖所示,如果a,c的絕對值相等,那么下列結論正確的是( )
4.實數a,b,c在數軸上對應點的位置如圖所示,如果a,c的絕對值相等,那么下列結論正確的是( )A.a+b>0 B.abc<0 C.c<-b D.b-a>0 組卷:87引用:3難度:0.7 -
5.在平面直角坐標系xOy中,直線y=kx與雙曲線
有公共點,則k的取值范圍是( )y=1xA.k>0 B.k<0 C.k≥0 D.k≤0 組卷:276引用:2難度:0.6 -
6.甲、乙兩名運動員的10次射擊成績(單位:環)如圖所示,甲、乙兩名運動員射擊成績的平均數依次記為
甲,x乙,射擊成績的方差依次記為s甲2,s乙2,則下列關系中完全正確的是( )x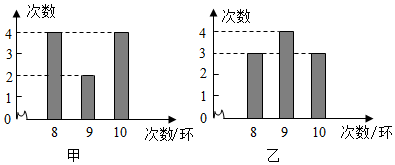
A. 甲=x乙,s甲2>s乙2xB. 甲=x乙,s甲2<s乙2xC. 甲>x乙,s甲2>s乙2xD. 甲<x乙,s甲2<s乙2x組卷:751引用:15難度:0.6 -
7.關于x的一元二次方程x2-(k+3)x+2k+1=0根的情況是( )
A.無實根 B.有實根 C.有兩個不相等實根 D.有兩個相等實根 組卷:476引用:7難度:0.7 -
8.某產品的盈利額(即產品的銷售價格與固定成本之差)記為y,購買人數記為x,其函數圖象如圖1所示.由于日前該產品盈利未達到預期,相關人員提出了兩種調整方案,如圖2,圖3中的實線分別為調整后y與x的函數圖象.給出下列四種說法,其中正確說法的序號是( )
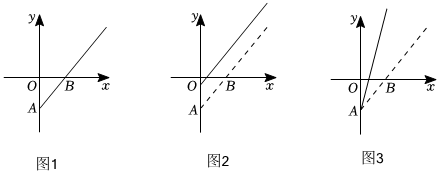
①圖2對應的方案是:保持銷售價格不變,并降低成本;
②圖2對應的方案是:提高銷售價格,并提高成本;
③圖3對應的方案是:提高銷售價格,并降低成本;
④圖3對應的方案是:提高銷售價格,并保持成本不變.A.①③ B.②③ C.①④ D.②④ 組卷:207引用:1難度:0.5
二、填空題(本題共16分,每題2分)
-
9.
在實數范圍內有意義,則x的取值范圍是:.2x+3組卷:214引用:3難度:0.7
三、解答題(共68分,第17-22題,每題5分,第23-26題,每題6分,第27-28題,每題7分)解答應寫出文字說明、演算步驟或證明過程.
-
27.如圖,AB=AC,∠BAC=90°,過點C作直線l⊥AC,點D,E是直線l上的動點(D在E的右側)且滿足DE=AB,連接BD,∠ABD的平分線與射線AE交于點F,與射線AC交于點G.
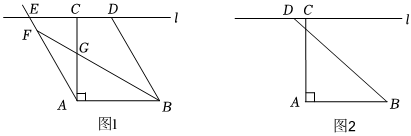
(1)如圖1,當點C在線段DE上,且∠CAE=30°時,若AB=6,求線段EF的長;
(2)如圖2,當點D在點C左側時,
①依題意補全圖形;
②用等式表示線段AG,CD,EF的數量關系,并證明.組卷:257引用:1難度:0.2 -
28.在平面直角坐標系xOy中,對于兩個圖形X,Y和直線y=m,若在圖形X上存在點A,在圖形Y上存在點B,使得點A和點B關于直線y=m對稱,就稱圖形X和Y互為m-關聯.
(1)若⊙O的半徑為1,點P(0,2)與⊙O為m-關聯,則m的值為 ;
(2)已知點A(4,3),射線OA與線段l:y=-2(-1≤x≤2)為t-關聯,求t的取值范圍;
(3)已知⊙O的半徑為2,直線與x軸,y軸分別交于點C,D,若⊙O關于y=m對稱的圖形S與線段CD互為2m-關聯,直接寫出m的取值范圍.y=33x-1組卷:234引用:1難度:0.1


