2022-2023學(xué)年浙江省寧波市南三縣八年級（下）期末數(shù)學(xué)試卷

一、選擇題（本大題共10小題，共30分）

• 1．若式子

  x

  -

  1

  有意義，則x的值可以為（　　）

  A．4

  B．-4

  C．-1

  D．0
  組卷：91引用：5難度：0.9

  解析

• 2．下列航天圖標，其文字上方的圖案是中心對稱圖形的是（　　）

  A． 中國探火	B． 中國火箭
  C． 中國行星探測	D． 航天神舟
  組卷：83引用：7難度：0.5

  解析

• 3．下列方程一定是一元二次方程的是（　　）

  A．2x-1=4x+3

  B．2x2+y-1=0

  C．2x2-1=3

  D．a(chǎn)x2+bx+c=0
  組卷：492引用：8難度：0.9

  解析

• 4．用反證法證明命題“在同一平面內(nèi)，若a⊥b,c⊥b,則a∥c”時，首先應(yīng)假設(shè)（　　）

  A．a(chǎn)∥b

  B．c∥b

  C．a(chǎn)與c相交

  D．a(chǎn)與b相交
  組卷：511引用：10難度：0.7

  解析

• 5．菱形具有而矩形不一定具有的性質(zhì)是（　　）

  A．對角相等	B．鄰角互補
  C．對角線互相平分	D．對角線平分一組對角
  組卷：114引用：2難度：0.7

  解析

• 6．若一元二次方程x²-2x+k=0有兩個不相等的實數(shù)根，則k的取值范圍是（　　）

  A．k＞1

  B．k＜1

  C．k＜1且k≠0

  D．k≥1
  組卷：1022引用：8難度：0.9

  解析

• 7．一場有19位同學(xué)參加的比賽，取前10名進決賽且所得分數(shù)互不相同．某同學(xué)知道自己的分數(shù)后要判斷是否能進決賽，他只需要知道這19位同學(xué)所得分數(shù)的（　　）

  A．平均數(shù)

  B．中位數(shù)

  C．眾數(shù)

  D．方差
  組卷：61引用：2難度：0.7

  解析

• 8．以下函數(shù)在自變量的取值范圍內(nèi)y隨x的增大而減小的是（　　）

  A．y=2x-1

  B． y = 1 3 x

  C． y = - 3 x （ x ＜ 0 ）

  D． y = 6 x （ x ＞ 0 ）
  組卷：363引用：3難度：0.5

  解析

三、解答題（本大題共8小題，共66分）

• 23．閱讀材料，根據(jù)上述材料解決以下問題：
  材料1：若一元二次方程 ax²+bx+c=0（a≠0）的兩個根為 x₁x₂，則

  x

  1

  +

  x

  2

  =

  -

  b

  a

  x

  1

  x

  2

  =

  c

  a

  
  材料2：已知實數(shù)m,n滿足 m²-m-1=0，n²-n-1=0，且m≠n,則 m,n 是方程x²-x-1=0 的兩個不相等的實數(shù)根．
  （1）材料理解：一元二次方程 3x²-6x+1=0 兩個根為 x₁x₂，則 x₁+x₂=

  ，x₁x₂=

  ．
  （2）應(yīng)用探究：已知實數(shù)m,n滿足 9m²-9m-1=0，9n²-9n-1=0，且m≠n,求 m²n+mn²的值．
  （3）思維拓展：已知實數(shù)s、t分別滿足 9s²+9s+1=0，t²+9t+9=0，其中st≠1且st≠0．求

  3

  st

  +

  9

  s

  +

  3

  t

  的值．
  組卷：724引用：1難度：0.5

  解析

• 24．定義：把能被一條對角線分成兩個全等直角三角形的四邊形叫做勾股四邊形．
  （1）矩形

  勾股四邊形（填“是”或“不是”）．
  （2）如圖在直角坐標系xOy中，直線y=-x+1與雙曲線

  y

  =

  -

  6

  x

  相交于A，B兩點，點P（-3，0）在x軸負半軸上，Q為直角坐標平面上一點．
  ①分別求出A、B兩點的坐標．
  ②當(dāng)四邊形APQB是平行四邊形時，如圖（Ⅰ），請證明?APQB是勾股四邊形．
  （3）在（2）的條件下，當(dāng)以A、B、P、Q為頂點的四邊形是勾股四邊形時，請直接寫出Q點的坐標．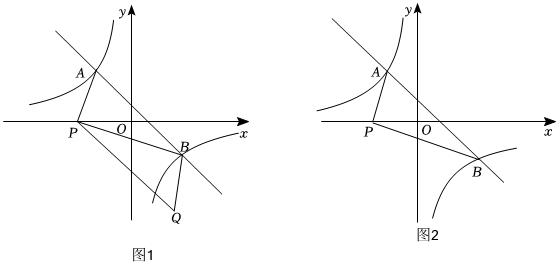
  ?
  組卷：617引用：3難度：0.5

  解析