2022-2023學(xué)年北京市101中學(xué)高一（下）期中數(shù)學(xué)試卷

一、選擇題共10小題，每小題4分，共40分.在每小題列出的四個(gè)選項(xiàng)中，選出符合題目要求的一項(xiàng).

• 1．sin（-150°）的值為（　　）

  A．- 1 2

  B． 1 2

  C．- 3 2

  D． 3 2
  組卷：309引用：20難度：0.9

  解析

• 2．已知tanα=

  1

  3

  ，則tan2α=（　　）

  A．- 4 3

  B． 4 3

  C．- 3 4

  D． 3 4
  組卷：150引用：4難度：0.9

  解析

• 3．已知向量

  a

  =（1，-2），

  b

  =（x,4），且

  a

  ∥

  b

  ，則|

  a

  -

  b

  |=（　　）

  A． 5 3

  B． 3 5

  C． 2 5

  D． 2 2
  組卷：179引用：12難度：0.9

  解析

• 4．下列函數(shù)中最小正周期為π的是（　　）
  ①f（x）=cosx?sinx；
  ②f（x）=cosx+sinx；
  ③

  f

  （

  x

  ）

  =

  sinx

  cosx

  ；
  ④f（x）=2sin²x

  A．①②

  B．②④

  C．①③④

  D．①②④
  組卷：202引用：3難度：0.8

  解析

• 5．在正方形ABCD中，E為AB的中點(diǎn)，F(xiàn)為CE的中點(diǎn)，則

  AF

  =（　　）

  A． 3 4 AB + 1 4 AD

  B． 1 4 AB + 3 4 AD

  C． 1 2 AB + AD

  D． 3 4 AB + 1 2 AD
  組卷：412引用：8難度：0.7

  解析

• 6．在△ABC中，角A，B，C所對(duì)的邊分別是a,b,c,已知a=2bcosC，則△ABC的形狀是（　　）

  A．等腰三角形	B．直角三角形
  C．等腰直角三角形	D．等腰或直角三角形
  組卷：399引用：15難度：0.9

  解析

三、解答題：共5小題，共55分.解答應(yīng)寫出文字說明、演算步驟或證明過程.

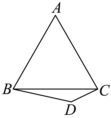• 19．在△ABC中，角A，B，C的對(duì)邊分別為a,b,c,

  3

  a

  =

  b

  （

  sin

  C

  +

  3

  cos

  C

  ）

  ．
  （1）求角B的大小；
  （2）若

  A

  =

  π

  3

  ，D為△ABC外一點(diǎn)，如圖DB=4，CD=2，求四邊形ABDC面積的最大值．
  組卷：172引用：3難度：0.6

  解析

• 20．給定正整數(shù)n≥2，設(shè)M={α|α=（t₁，t₂，…，t_n），t_k∈{0，1}，k=1，2，…，n}為n維0-1向量α的集合．對(duì)于集合M中的任意元素β=（x₁，x₂，?，x_n）和γ=（y₁，y₂，?，y_n），定義它們的內(nèi)積為β?γ=x₁y₁+x₂y₂+?+x_ny_n．
  設(shè)A?M．且集合A={α_i|α_i=（t_i1，t_i2，…，t_in），i-1，2，?，n}，對(duì)于A中任意元素α_i，α_j，若

  α

  i

  ?

  α

  j

  =

  p , i = j ,

  q , i ≠ j ,

  則稱A具有性質(zhì)H（p,q）．
  （1）當(dāng)n=3時(shí)，判斷集合A={（1，1，0），（1，0，1），（0，1，1）}是否具有性質(zhì)H（2，0）？說明理由；
  （2）當(dāng)n=4時(shí)，判斷是否存在具有性質(zhì)H（p,q）的集合A，若存在求出p,q,若不存在請(qǐng)證明；
  （3）若集合A具有性質(zhì)H（p,1），證明：t_1j+t_2j+?+t_nj=p（j=1，2，?，n）．
  組卷：64引用：3難度：0.4

  解析