2022-2023學(xué)年江蘇省南京市建鄴區(qū)八年級(jí)（上）期末數(shù)學(xué)試卷

一、選擇題（本大題共6小題，每小題2分，共16分，在每小題所給出的四個(gè)選項(xiàng)中，恰有一項(xiàng)是符合題目要求的，請(qǐng)將正確選項(xiàng)前的字母代號(hào)填涂在答題卡相應(yīng)位置上）

• 1．4的算術(shù)平方根為（　　）

  A．-2

  B．2

  C．±2

  D． 2
  組卷：1118引用：40難度：0.9

  解析

• 2．在平面直角坐標(biāo)系中，把點(diǎn)（2，3）向上平移1個(gè)單位，再向左平移2個(gè)單位，得到的點(diǎn)的坐標(biāo)是（　　）

  A．（3，1）

  B．（0，4）

  C．（4，4）

  D．（1，1）
  組卷：1882引用：13難度：0.6

  解析

• 3．下列無(wú)理數(shù)中，在-2與1之間的是（　　）

  A．- 5

  B．- 3

  C． 3

  D． 5
  組卷：1359引用：92難度：0.9

  解析

• 4．在平面直角坐標(biāo)系中，已知點(diǎn)P（m-1，m+2）（m是任意實(shí)數(shù)），則點(diǎn)P不會(huì)落在（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  組卷：1194引用：3難度：0.8

  解析

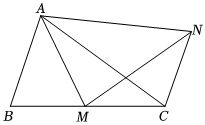• 5．如圖，△ABC≌△AMN，點(diǎn)M在BC上，連接CN，下列結(jié)論：
  ①AM平分∠BMN
  ②∠CMN=∠BAM
  ③∠MAC=∠MNC
  其中，所有正確結(jié)論的序號(hào)是（　　）

  A．①②

  B．②③

  C．①③

  D．①②③
  組卷：614引用：1難度：0.7

  解析

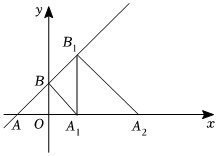• 6．如圖，在平面直角坐標(biāo)系中，一次函數(shù)y=x+

  2

  的圖象交x軸于點(diǎn)A，交y軸于點(diǎn)B，點(diǎn)A₁，A₂，A₃?在x軸上，點(diǎn)B₁，B₂，B₃?在函數(shù)圖象上，A₁B₁，A₂B₂，A₃B₃?均垂直于x軸，若△A₁OB，△A₂A₁B₁，△A₃A₂B₂?均為等腰直角三角形，則△A₅A₄B₄的面積是（　　）

  A．16

  B．64

  C．256

  D．1024
  組卷：573引用：4難度：0.5

  解析

二、填空題（本大題共10小題，每小題2分，共20分，不需寫(xiě)出解答過(guò)程，請(qǐng)把答案直接填寫(xiě)在答題卡相應(yīng)位置上）

• 7．8的立方根是

  ．
  組卷：4834引用：172難度：0.7

  解析

• 8．點(diǎn)P在第二象限，且到x軸，y軸的距離分別為2、3．則點(diǎn)P的坐標(biāo)是

  ．
  組卷：1572引用：7難度：0.7

  解析

三、解答題（本大題共10小題，共64分，請(qǐng)?jiān)诖痤}卡指定區(qū)域內(nèi)作答，解答時(shí)應(yīng)寫(xiě)出文字說(shuō)明、證明過(guò)程或演算步驟）

• 25．【數(shù)學(xué)概念】
  如果三角形的三邊長(zhǎng)分別為a,b,c,且2a²+b²=c²，那么我們稱這樣的三角形為“奇妙三角形”．
  【概念理解】
  （1）若△ABC是“奇妙三角形”，∠C＞90°，AB=5，AC=3，則BC=

  ．
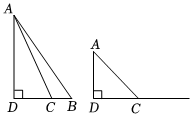
  （2）如圖①△ABD，∠D=90°，點(diǎn)C在BD上，連接AC，AD=4．CD=3，若△ABC是“奇妙三角形”，求BC的長(zhǎng)．
  【靈活運(yùn)用】
  （3）如圖②，在Rt△ACD，∠D=90°，AD=m,CD=n,點(diǎn)B在邊DC的延長(zhǎng)線上，當(dāng)BC=

  時(shí)（用含m,n的代數(shù)式表示），△ABC是“奇妙三角形”．
  組卷：801引用：3難度：0.5

  解析

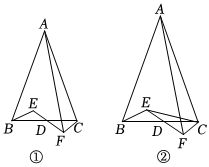• 26．如圖①，在△ABC中，AB=AC，D是BC的中點(diǎn)，E為△ABC內(nèi)一點(diǎn)，連接ED并延長(zhǎng)到F，使得ED=DF，連接AF、CF．
  （1）求證：BE∥CF；
  （2）若∠EBD=

  1

  2

  ∠BAC，求證：AF²=AB²+BE²；
  （3）如圖②連接，探索當(dāng)∠BEC與∠BAC滿足什么數(shù)量關(guān)系時(shí)，AC=AF，并說(shuō)明理由．
  組卷：703引用：3難度：0.3

  解析