2022-2023學(xué)年安徽省安慶市潛山市九年級(jí)（上）第一次月考數(shù)學(xué)試卷

一、選擇題（本大題共10小題，每小題4分，滿分40分）

• 1．對(duì)于二次函數(shù)y=-2（x+3）²的圖象，下列說(shuō)法正確的是（　　）

  A．開口向上

  B．對(duì)稱軸是直線x=-3

  C．當(dāng)x＞-4時(shí)，y隨x的增大而減小

  D．頂點(diǎn)坐標(biāo)為（-2，-3）
  組卷：5527引用：24難度：0.5

  解析

• 2．已知線段AB=10，點(diǎn)C是AB的黃金分割點(diǎn)，則AC=（　　）

  A．5 5 -5	B．15-5 5
  C．5 5 -5或15-5 5	D．以上都不對(duì)
  組卷：315引用：5難度：0.8

  解析

• 3．在平面直角坐標(biāo)系中，拋物線y=（x+5）（x-3）經(jīng)變換后得到拋物線y=（x+3）（x-5），則這個(gè)變換可以是（　　）

  A．向左平移2個(gè)單位	B．向右平移2個(gè)單位
  C．向左平移8個(gè)單位	D．向右平移8個(gè)單位
  組卷：859引用：29難度：0.6

  解析

• 4．已知三條線段長(zhǎng)分別是3，4，12，若再添加一條新線段，使這四條線段能成比例，則這條新線段長(zhǎng)不可能是（　　）

  A．1

  B．9

  C．20

  D．16
  組卷：250引用：2難度：0.7

  解析

• 5．下面表格中的數(shù)據(jù)是二次函數(shù)y=ax²+bx+c的幾組對(duì)應(yīng)值．根據(jù)表中的數(shù)據(jù)我們可以判斷．當(dāng)y=ax²+bx+c＞0時(shí)，自變量x的取值范圍是（　　）
  

  x	…	-1	0	1	2	3	4	…
  y	…	0	-3	-4	-3	0	5	…

  A．x＞1

  B．x＜-1或x＞3

  C．x＞5

  D．-1＜x＜3
  組卷：207引用：3難度：0.7

  解析

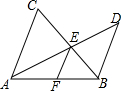• 6．如圖，AC∥BD，AD與BC交于點(diǎn)E，過(guò)點(diǎn)E作EF∥BD，交線段AB于點(diǎn)F，則下列各式錯(cuò)誤的是（　　）

  A． AF BF = AE DE	B． BF AF = BE CE
  C． AE AD + BE BC =1	D． AF BF = CE DE
  組卷：2193引用：4難度：0.7

  解析

• 7．若拋物線y=2（x+m-1）²-3m+6的頂點(diǎn)在第二象限，則m的取值范圍是（　　）

  A．m＞1

  B．m＜2

  C．1＜m＜2

  D．-2＜m＜-1
  組卷：483引用：2難度：0.6

  解析

七、（本大題共1小題，每小題12分，總計(jì)12分）

• 22．如圖，一次函數(shù)y=k₁x+b的圖象與x軸，y軸分別交于A，B兩點(diǎn)，與反比例函數(shù)y=

  k

  2

  x

  的圖象分別交于C，D兩點(diǎn)，若點(diǎn)C坐標(biāo)是（3，6），且AB=BC．
  （1）求一次函數(shù)y=k₁x+b與反比例函數(shù)y=

  k

  2

  x

  的解析式；
  （2）求△COD的面積；
  （3）直接寫出當(dāng)x取何值時(shí)，k₁x+b

  ＜

  k

  2

  x

  ．
  組卷：566引用：2難度：0.6

  解析

八、（本大題共1小題，每小題14分，總計(jì)14分）

• 23．如圖，拋物線y=x²+bx+c與x軸交于A，B兩點(diǎn)，與y軸交于點(diǎn)C，直線y=-x+4經(jīng)過(guò)點(diǎn)B，C．
  （1）求拋物線的表達(dá)式．
  （2）直線x=m（其中0＜m＜4）與線段BC交于點(diǎn)P，與拋物線交于點(diǎn)Q，連接OQ，當(dāng)線段PQ長(zhǎng)的最大時(shí)，求證：四邊形OCPQ是平行四邊形．
  （3）在（2）的條件下，連接AQ，過(guò)點(diǎn)Q的直線與拋物線交于點(diǎn)D，若∠AQP=∠DQP，求點(diǎn)D的坐標(biāo)．
  組卷：314引用：5難度：0.3

  解析