2022-2023學年天津市南開中學高三（上）統練數學試卷（八）

一、單選題

• 1．設集合A={-1，0，3}，B={0，1，2}，C={x∈R|-2≤x＜2}，則（A∪B）∩C=（　　）

  A．{1}

  B．{-2，3}

  C．{-1，0，1}

  D．{-1，0，1，2}
  組卷：188引用：2難度：0.8

  解析

• 2．已知等比數列{a_n}的首項為a₁，公比為q,則“a₁（q-1）＞0”是“數列{a_n}為遞增數列”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．既不充分也不必要條件
  組卷：72引用：3難度：0.5

  解析

• 3．函數

  f

  （

  x

  ）

  =

  sinx

  +

  x

  cosx

  +

  x

  2

  在[-π，π]上的圖像大致為（　　）

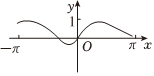
  A．	B．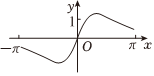
  C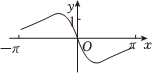．	D．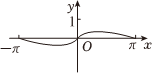
  組卷：504引用：6難度：0.8

  解析

• 4．設

  a

  =

  lo

  g

  2

  3

  ，

  b

  =

  lo

  g

  4

  5

  ，

  c

  =

  2

  -

  0

  .

  1

  ，則a,b,c的大小關系為（　　）

  A．a＞b＞c

  B．b＞a＞c

  C．c＞b＞a

  D．a＞c＞b
  組卷：471引用：2難度：0.7

  解析

• 5．已知數列{a_n}的前n項和為S_n，a₁=1，S_n+S_n-1=4n²（n≥2，n∈N^*），則a₁₀₀=（　　）

  A．414

  B．406

  C．403

  D．393
  組卷：322引用：4難度：0.5

  解析

• 6．已知等比數列{a_n}的各項均為正數，且a₁+a₃=20，a₃+a₅=5，則使得a₁a₂…a_n＜1成立的正整數n的最小值為（　　）

  A．8

  B．9

  C．10

  D．11
  組卷：296引用：3難度：0.7

  解析

三、解答題

• 19．已知等差數列{a_n}的前n項和為S_n，且S₄=4S₂，a_2n=2a_n+1（n∈N^*）．數列{b_n}為等比數列，且b₂-a₂=1，a₅-b₃=1．
  （1）求數列{a_n}和{b_n}的通項公式；
  （2）求

  n

  ∑

  k

  =

  1

  a

  k

  b

  k

  ．
  （3）求證：

  n

  ∑

  k

  =

  1

  k

  2

  a

  k

  ?

  a

  k

  +

  1

  =

  n

  （

  n

  +

  1

  ）

  2

  a

  n

  +

  1

  ．
  組卷：71引用：3難度：0.5

  解析

• 20．已知函數f（x）=

  - x 3 + x 2 + 1 ， x ＜ 0

  e x - ax , x ≥ 0

  ，g（x）=lnx-ax+m.
  （1）當a=3時，求函數f（x）的單調區間；
  （2）若不等式f（x）＞g（x）對任意的正實數x都成立，求實數m的最大整數；
  （3）當a＞0時，若存在實數m,n∈[0，2]，且|m-n|≥1，使得f（m）=f（n），求證：e-1≤a≤e²-e
  組卷：472引用：4難度：0.1

  解析