《第1章 三角函數(shù)》2006年單元測試卷（揚(yáng)子中學(xué)）

一、選擇題（每小題5分，共60分，請將所選答案填在括號內(nèi)）

• 1．設(shè)a＜0，角α的終邊經(jīng)過點(diǎn)P（-3a,4a），那么sinα+2cosα的值等于（　　）

  A． 2 5

  B．- 2 5

  C． 1 5

  D．- 1 5
  組卷：346引用：17難度：0.9

  解析

• 2．若cos（π+α）=-

  1

  2

  ，

  3

  2

  π＜α＜2π，則sin（2π-α）等于（　　）

  A．- 3 2

  B． 3 2

  C． 1 2

  D．± 3 2
  組卷：615引用：13難度：0.9

  解析

• 3．已知sinα＞sinβ，那么下列命題成立的是（　　）

  A．若α、β是第一象限角，則cosα＞cosβ

  B．若α、β是第二象限角，則tanα＞tanβ

  C．若α、β是第三象限角，則cosα＞cosβ

  D．若α、β是第四象限角，則tanα＞tanβ
  組卷：1879引用：28難度：0.9

  解析

• 4．若sinx+cosx=1，那么sinⁿx+cosⁿx的值是（　　）

  A．1

  B．0

  C．-1

  D．不能確定
  組卷：91引用：2難度：0.9

  解析

• 5．函數(shù)y=-xcosx的部分圖象是（　　）

  A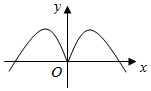．	B．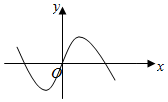
  C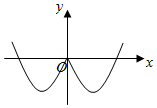．	D．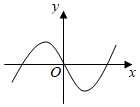
  組卷：976引用：67難度：0.9

  解析

• 6．函數(shù)y=cos²x-sinx的值域是（　　）

  A． [ - 1 ， 5 4 ]

  B． [ 1 ， 5 4 ]

  C．[0，2]

  D．[-1，1]
  組卷：1133引用：9難度：0.9

  解析

• 7．已知：函數(shù)y=Asin（ωx+φ），在同一周期內(nèi)，當(dāng)

  x

  =

  π

  12

  時取最大值y=4；當(dāng)

  x

  =

  7

  π

  12

  時，取最小值y=-4，那么函數(shù)的解析式為：（　　）

  A． y = 4 sin （ 2 x + π 3 ）	B． y = - 4 sin （ 2 x + π 3 ）
  C． y = 4 sin （ 4 x + π 3 ）	D． y = - 4 sin （ 4 x + π 3 ）
  組卷：88引用：1難度：0.7

  解析

三、解答題（本大題6小題，共74分，解答應(yīng)寫出文字說明，證明過程或演算步驟）

• 21．已知y=Asin（ωx+φ），（A＞0，ω＞0，|φ|＜π）的圖象過點(diǎn)P（

  π

  12

  ，0）圖象上與點(diǎn)P最近的一個頂點(diǎn)是Q（

  π

  3

  ，5）．
  （1）求函數(shù)的解析式；
  （2）求使y≤0的x的取值范圍．
  組卷：85引用：1難度：0.3

  解析

• 22．函數(shù)的性質(zhì)通常指函數(shù)的定義域、值域、周期性、單調(diào)性、奇偶性等，請選擇適當(dāng)?shù)奶骄宽樞颍芯亢瘮?shù)f（x）=

  1

  -

  sinx

  +

  1

  +

  sinx

  的性質(zhì)，并在此基礎(chǔ)上，作出其在[-π，π]的草圖．
  組卷：117引用：4難度：0.5

  解析