2022-2023學(xué)年遼寧省鐵嶺市六校高二(下)期末數(shù)學(xué)試卷
發(fā)布:2024/7/3 8:0:9
一、選擇題:本題共8小題,每小題5分,共40分.在每小題給出的四個(gè)選項(xiàng)中,只有一項(xiàng)是符合題目要求的.
-
1.命題“?x0∈N,
”的否定是( )ex0-x0-1≤0A.?x0∈N, ex0-x0-1>0B.?x∈N,ex-x-1>0 C.?x∈N,ex-x-1≤0 D.?x?N,ex-x-1≤0 組卷:72引用:2難度:0.7 -
2.已知數(shù)列-6,66,-666,6666,-66666,…,則該數(shù)列的第2024項(xiàng)為( )
A. -32(102024-1)B. 32(102024-1)C. -23(102024-1)D. 23(102024-1)組卷:212引用:3難度:0.7 -
3.函數(shù)
的導(dǎo)數(shù)f′(x)=( )f(x)=cosxxA. xsinx-cosxx2B. -xsinx-cosxx2C. xsinx+cosxx2D. -xsinx+cosxx2組卷:270引用:4難度:0.8 -
4.若公比為-3的等比數(shù)列的前2項(xiàng)和為10,則該等比數(shù)列的第3項(xiàng)為( )
A.15 B.-15 C.45 D.-45 組卷:142引用:5難度:0.9 -
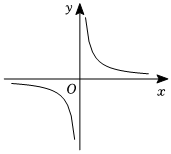 5.已知函數(shù),g(x)=x2+1,則如圖對(duì)應(yīng)的函數(shù)解析式可能是( )f(x)=x+1x
5.已知函數(shù),g(x)=x2+1,則如圖對(duì)應(yīng)的函數(shù)解析式可能是( )f(x)=x+1xA.y=f(x)+g(x) B.y=f(x)-g(x) C.y=[f(x)]2g(x) D. y=f(x)g(x)組卷:26引用:3難度:0.6 -
6.設(shè)Tn是數(shù)列{an}的前n項(xiàng)積,則“
”是“{an}是等差數(shù)列”的( )Tn=3nA.充分不必要條件 B.必要不充分條件 C.充要條件 D.既不充分也不必要條件 組卷:34引用:4難度:0.7 -
7.若存在直線(xiàn)y=kx+b,使得函數(shù)F(x)和G(x)對(duì)其公共定義域上的任意實(shí)數(shù)x都滿(mǎn)足F(x)≥kx+b≥G(x),則稱(chēng)此直線(xiàn)y=kx+b為F(x)和G(x)的“隔離直線(xiàn)”.已知函數(shù)f(x)=x2,g(x)=alnx(a>0),若f(x)和g(x)存在唯一的“隔離直線(xiàn)”,則a=( )
A. eB. 2eC.e D.2e 組卷:153引用:3難度:0.5
四、解答題:本題共6小題,共70分.解答應(yīng)寫(xiě)出文字說(shuō)明、證明過(guò)程或演算步驟.
-
21.已知公差為-2的等差數(shù)列{an}的前n項(xiàng)和為Sn,且S5=-5.
(1)求{an}的通項(xiàng)公式;
(2)若數(shù)列的前n項(xiàng)和為T(mén)n,證明:{1anan+1}為定值.Tn-12an+1組卷:78引用:3難度:0.5 -
22.已知函數(shù)
.f(x)=32x2-x-xlnx
(1)求f(x)的圖象在點(diǎn)(1,f(1))處的切線(xiàn)方程;
(2)證明:f(x)+cosx-1>0.組卷:43引用:2難度:0.4


