2023-2024學年北京市101中學高三（上）統練數學試卷（五）

一、選擇題共10小題。在每小題列出的四個選項中，選出符合題目要求的一項。

• 1．已知集合P={x|-1≤x≤1}，

  Q

  =

  {

  x

  ∈

  N

  |

  x

  x

  -

  2

  ≤

  0

  }

  ，則P∩Q=（　　）

  A．{x|0≤x≤1}

  B．{x|-1≤x≤0}

  C．{0，1，2}

  D．{0，1}
  組卷：29引用：2難度：0.7

  解析

• 2．等差數列{a_n}中，a₂=3，a₃+a₄=9則a₁a₆的值為（　　）

  A．14

  B．18

  C．21

  D．27
  組卷：157引用：17難度：0.9

  解析

• 3．在△ABC中，角A、B、C所對的邊分別為a、b、c,已知a=3，b=

  6

  ，A=

  π

  3

  ，則角B等于（　　）

  A． π 4

  B． 3 π 4

  C． π 4 或 3 π 4

  D．以上都不對
  組卷：89引用：9難度：0.9

  解析

• 4．將y=2cos（

  x

  3

  +

  π

  6

  ）的圖象通過平移變換，得到一個奇函數的圖象，則這個變換可以是（　　）

  A．左移 π 3 個單位	B．右移 π 3 個單位
  C．左移π個單位	D．右移π個單位
  組卷：140引用：4難度：0.9

  解析

• 5．在△ABC中，“A＞30°”是“sinA＞

  1

  2

  ”的（　　）

  A．充分而不必要條件	B．必要而不充分條件
  C．充分必要條件	D．既不充分也必要條件
  組卷：330引用：45難度：0.9

  解析

• 6．在下列函數中，最小值是2的是（　　）

  A．y= x 2 + 2 x

  B．y= x + 2 x + 1 （x＞0）

  C．y=sinx+ 1 sinx ，x∈（0， π 2 ）

  D．y=7x+7-x
  組卷：190引用：5難度：0.9

  解析

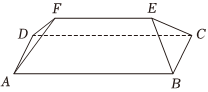• 7．坡屋頂是我國傳統建筑造型之一，蘊含著豐富的數學元素．安裝燈帶可以勾勒出建筑輪廓，展現造型之美．如圖，某坡屋頂可視為一個五面體，其中兩個面是全等的等腰梯形，兩個面是全等的等腰三角形．若AB=25m,BC=AD=10m,且等腰梯形所在的平面、等腰三角形所在的平面與平面ABCD的夾角的正切值均為

  14

  5

  ，則該五面體的所有棱長之和為（　　）

  A．102m

  B．112m

  C．117m

  D．125m
  組卷：305引用：8難度：0.4

  解析

三、解答題共6小題。解答應寫出文字說明、演算步驟或證明過程。

• 20．已知函數f（x）=e^ax（x-1）²．
  （1）若a=1，求f（x）在（0，f（0））處切線方程；
  （2）求f（x）的極大值與極小值；
  （3）證明：存在實數M，當a＞0時，函數y=f（x）-M有三個零點．
  組卷：451引用：7難度：0.5

  解析

• 21．對于一個n行n列的數表A_n×n（n≥2），用a_i,j表示數表中第i行第j列的數，其中a_i,j∈Z（i,j=1，2，?，n），且數表A_n×n滿足以下兩個條件：
  ①

  n

  ∑

  j

  =

  1

  a

  1

  ，

  j

  =

  n

  ；
  ②a_i+1，j+1=a_i,j，規定a_i+1，n+1=a_i+1，1（i=1，2，?，n-1，j=1，2，?，n）．
  （Ⅰ）已知數表A_3×3中，a_1，1=3，a_1，2=-1．寫出a_1，3，a_2，2，a_3，1的值；
  （Ⅱ）若a_1，1+?+a_1，k-k=max{a_1，1-1，a_1，1+a_1，2-2，?，a_1，1+?+a_1，n-n}（k∈{1，2，?，n}），其中maxM表示數集M中最大的數．規定a_1，n+1=a_1，1．證明：a_1，k+1-1≤0；
  （Ⅲ）證明：存在m∈{1，2，?，n}，對于任意l∈{1，2，?，n}，有a_m,1+a_m,2+?+a_m,l≤l.
  組卷：114引用：5難度：0.1

  解析