2023-2024學年廣東省佛山市順德區華僑中學高三（上）月考數學試卷（8月份）

一、單選題（每小題5分）

• 1．已知U=R，A={x|-1＜x＜3}，B={x|x≤2}，則?_U（A∪B）=（　　）

  A．（-∞，-1]∪（2，+∞）	B．（-∞，-1）∪[2，+∞）
  C．[3，+∞）	D．（3，+∞）
  組卷：444引用：10難度：0.8

  解析

• 2．已知復數z滿足（z+2i）（2-i）=5，則z的共軛復數

  z

  =（　　）

  A．2-i

  B．2+i

  C．-2+i

  D．-2-i
  組卷：122引用：7難度：0.8

  解析

• 3．若

  （

  x

  +

  2

  ）

  4

  =

  a

  4

  x

  4

  +

  a

  3

  x

  3

  +

  a

  2

  x

  2

  +

  a

  1

  x

  +

  a

  0

  ，則a₄-a₃+a₂-a₁+a₀=（　　）

  A．1

  B．-1

  C．15

  D．-15
  組卷：240引用：4難度：0.9

  解析

• 4．已知曲線y=axe^x+lnx在點（1，ae）處的切線方程為y=3x+b,則（　　）

  A．a=e,b=-2

  B．a=e,b=2

  C．a=e-1，b=-2

  D．a=e-1，b=2
  組卷：521引用：13難度：0.7

  解析

• 5．設公差不為零的等差數列{a_n}的前n項和為S_n，

  a

  4

  =

  1

  2

  a

  5

  ，則

  S

  9

  S

  4

  =（　　）

  A．15

  B．1

  C．-1

  D．-9
  組卷：387引用：10難度：0.7

  解析

• 6．現隨機安排甲、乙等4位同學參加校運會跳高、跳遠、投鉛球比賽，要求每位同學參加一項比賽，每項比賽至少一位同學參加，事件A=“甲參加跳高比賽”，事件B=“乙參加跳高比賽”，事件C=“乙參加跳遠比賽”，則（　　）

  A．事件A與B相互獨立	B．事件A與C為互斥事件
  C． P （ C | A ） = 5 12	D． P （ B | A ） = 1 9
  組卷：508引用：21難度：0.5

  解析

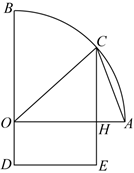• 7．如圖，已知OAB是半徑為2km的扇形，OA⊥OB，C是弧AB上的動點，過點C作CH⊥OA，垂足為H，某地區欲建一個風景區，該風景區由△AOC和矩形ODEH組成，且OH=2OD，則該風景區面積的最大值為（　　）

  A． 5 2 k m 2

  B． 11 4 k m 2

  C．3km2

  D． 17 8 k m 2
  組卷：173引用：3難度：0.6

  解析

四、解答題

• 21．為了“讓廣大青少年充分認識到毒品的危害性，切實提升青少年識毒防毒拒毒意識”，我市組織開展青少年禁毒知識競賽，團員小明每天自覺登錄“禁毒知識競賽APP”，參加各種學習活動，同時熱衷于參與四人賽．每局四人賽是由網絡隨機匹配四人進行比賽，每題回答正確得20分，第1個達到100分的比賽者獲得第1名，贏得該局比賽，該局比賽結束．每天的四人賽共有20局，前2局是有效局，根據得分情況獲得相應名次，從而得到相應的學習積分，第1局獲得第1名的得3分，獲得第2、3名的得2分，獲得第4名的得1分；第2局獲得第1名的得2分，獲得第2、3、4名的得1分；后18局是無效局，無論獲得什么名次，均不能獲得學習積分．經統計，小明每天在第1局四人賽中獲得3分、2分、1分的概率分別為

  1

  4

  ，

  1

  2

  ，

  1

  4

  ，在第2局四人賽中獲得2分、1分的概率分別為

  1

  4

  ，

  3

  4

  ．
  （1）設小明每天獲得的得分為X，求X的分布列和數學期望；
  （2）若小明每天賽完20局，設小明在每局四人賽中獲得第1名從而贏得該局比賽的概率為

  1

  4

  ，每局是否贏得比賽相互獨立，請問在每天的20局四人賽中，小明贏得多少局的比賽概率最大？
  組卷：75引用：2難度：0.6

  解析

• 22．已知函數f（x）=e^x-ax,g（x）=ln（x+2）-a,其中e為自然對數的底數，a∈R．
  （1）當a＞0時，函數f（x）有極小值f（1），求a；
  （2）證明：f'（x）＞g（x）恒成立；
  （3）證明：

  ln

  2

  +

  （

  ln

  3

  2

  ）

  2

  +

  （

  ln

  4

  3

  ）

  3

  +

  …

  +

  （

  ln

  n

  +

  1

  n

  ）

  n

  ＜

  e

  e

  -

  1

  ．
  組卷：669引用：4難度：0.6

  解析