當前位置：試卷中心 > 試卷詳情

2021-2022學年四川省甘孜州高二（下）期末數學試卷（理科）

發布：2024/4/20 14:35:0

1．已知集合A={x∈Z|-1＜x＜1}?，集合B={-2，0，2}?，則A∩B?（　　）
A．{0}? B．{-1，0，1}? C．0 D．（-1，1）?
組卷：5引用：1難度：0.9
解析
2．已知i是虛數單位，復數
1
-
2
i
i
=（　　）
A．2-i B．2+i C．-2+i D．-2-i
組卷：56引用：3難度：0.9
解析
3．已知條件p：2^x＞1的解集，條件q：函數y=
x
-
3
的定義域，則p是q的（　　）
A．充分不必要條件 B．必要不充分條件
C．充要條件 D．既不充分也不必要條件
組卷：7引用：1難度：0.9
解析
4．雙曲線的方程為x²-
y
2
4
=1?，則該雙曲線的離心率為（　　）
A．
5
5
? B．
2
5
5
? C．
5
2
? D．
5
?
組卷：8引用：2難度：0.7
解析
5．等差數列{a_n}?的前n?項和為S_n，a₂+a₅+a₈=21?，則S₉=?（　　）
A．42 B．56 C．63 D．70
組卷：4引用：1難度：0.7
解析
6．若sin（
π
4
-α）=
3
5
?，則sin2α=?（　　）
A．
-
7
25
? B．
-
24
25
? C．
7
25
? D．
24
25
?
組卷：25引用：2難度：0.8
解析
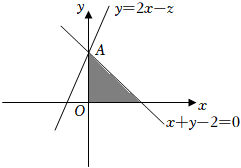7．若變量x、y?滿足約束條件
x
≥
0
y
≥
0
x
+
y
-
2
≤
0
?，則z=2x-y?的最小值為（　　）
A．-5? B．-2? C．0 D．1
組卷：0引用：2難度：0.7
解析

21．已知函數f（x）=lnx-ax+1（a∈R）?
（1）討論函數f（x）?的單調性；
（2）若a=-2?，是否存在實數m（m∈N^*）?，都有f（x）≤m（x+1）?恒成立，若存在求出實數m?的最小值，若不存在說明理由．
組卷：124引用：6難度：0.5
解析
22．在直角坐標系xOy?中，直線l?的參數方程為
x
=
3
2
t
y
=
1
+
1
2
t
?（t?為參數），在以O?為極點，x?軸非負半軸為極軸的極坐標系中，曲線C?的極坐標方程為ρ=2sinθ-2cosθ?
（1）求直線l?的普通方程與曲線C?的直角坐標方程；
（2）若直線l?與y?軸的交點為P?，直線l?與曲線C?的交點為A，B?，求|PA|?|PB|?的值．
組卷：25引用：4難度：0.5
解析