2014年4月全國100所名校單元測試示范卷數學（四）導數及其應用（文科）

一、選擇題：本大題共12小題，每小題5分，共60分.在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．已知f（x）=cosx,則f′（

  5

  π

  6

  ）等于（　　）

  A． 3 2

  B．- 3 2

  C． 1 2

  D．- 1 2
  組卷：176引用：2難度：0.9

  解析

• 2．已知點A是曲線y=

  3

  ln x（x≥1）上的動點，在點A處的切線傾斜角為θ，則θ的取值范圍是（　　）

  A．[0， π 2 ]

  B．[0， π 3 ]

  C．（0， π 3 ]

  D．[ π 3 ， π 2 ）
  組卷：107引用：2難度：0.9

  解析

• 3．已知函數f（x）=

  4

  3

  x³-

  1

  x

  的導函數為f′（x），則f′（x）的最小值為（　　）

  A．1

  B．2

  C．4

  D．8
  組卷：148引用：2難度：0.9

  解析

• 4．若函數f（x）=x³-3x+m恰有2個不同的零點，則實數m的值為（　　）

  A．±2

  B．±1

  C．-2或1

  D．-1或2
  組卷：150引用：2難度：0.9

  解析

• 5．函數f（x）=x+2cosx在區間[0，

  π

  2

  ]上取最小值時，x的值為（　　）

  A．0

  B． π 6

  C． π 3

  D． π 2
  組卷：100引用：4難度：0.9

  解析

• 6．a＞3，則方程x³-ax²+1=0在（0，2）上恰好有（　　）

  A．0個根

  B．1個根

  C．2個根

  D．3個根
  組卷：67引用：5難度：0.9

  解析

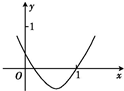• 7．如圖是二次函數f（x）=

  1

  2

  x²-bx+c的部分圖象，則函數g（x）=ln x+f′（x）的零點所在的區間是（　　）

  A．（ 1 4 ， 1 2 ）

  B．（ 1 2 ，1）

  C．（1，2）

  D．（2，3）
  組卷：140引用：3難度：0.7

  解析

三、解答題：本大題共6小題，共70分.解答應寫出必要的文字說明、證明過程及演算步驟.

• 21．已知函數y=f（x）=-x³+ax²+b…（a,b∈R）．
  （Ⅰ）當a＞0時，若f（x）滿足：y_極小值=1，y_極大值=

  31

  27

  ，試求f（x）的解析式；
  （Ⅱ）若x∈[0，1]時，y=f（x）圖象上的任意一點處的切線斜率k滿足：|k|≤1，求a的取值范圍．
  組卷：39引用：3難度：0.5

  解析

• 22．已知函數f（x）=ax²-ln x.
  （1）求函數的單調區間與最值；
  （2）當a=1時，函數g（x）=1-

  f

  （

  x

  ）

  x

  2

  ，求證：

  ln

  2

  2

  4

  +

  ln

  3

  3

  4

  +…+

  lnn

  n

  4

  ＜

  1

  2

  e

  ．（其中e為自然對數的底數）
  組卷：67引用：1難度：0.3

  解析