2022-2023學年重慶外國語學校高三（上）期中數學試卷

一、選擇題：本大題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．已知集合M={x|x²-x-6＞0}，集合N={x|ln（x-1）＞0}，則（?_RM）∩N=（　　）

  A．（3，+∞）

  B．（1，2]

  C．（2，3]

  D．（1，3）
  組卷：14引用：2難度：0.7

  解析

• 2．已知復數z滿足z+

  z

  =6，且（z-

  z

  ）?i³=-8，則z在復平面內對應的點位于（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  組卷：35引用：3難度：0.8

  解析

• 3．設隨機變量X～N（μ，σ²），則“μ≥1”是“P（X＜2）＜

  1

  2

  ”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．既不充分也不必要條件
  組卷：102引用：3難度：0.8

  解析

• 4．1883年，德國數學家康托提出了三分康托集，亦稱康托爾集．如圖是其構造過程的圖示，其詳細構造過程可用文字描述為：第一步，把閉區間[0，1]平均分成三段，去掉中間的一段，剩下兩個閉區間

  [

  0

  ，

  1

  3

  ]

  和

  [

  2

  3

  ，

  1

  ]

  ；第二步，將剩下的兩個閉區間分別平均分為三段，各自去掉中間的一段，剩下四段閉區間：

  [

  0

  ，

  1

  9

  ]

  ，

  [

  2

  9

  ，

  1

  3

  ]

  ，

  [

  2

  3

  ，

  7

  9

  ]

  ，

  [

  8

  9

  ，

  1

  ]

  ；如此不斷的構造下去，最后剩下的各個區間段就構成了三分康托集．若經歷n步構造后，所有去掉的區間長度和為（　　）（注：（a,b）或（a,b]或[a,b）或[a,b]的區間長度均為b-a）
  

  A．1- （ 1 3 ） n

  B．1- （ 2 3 ） n

  C．1-2× （ 1 3 ） n

  D．1-2× （ 2 3 ） n
  組卷：44引用：4難度：0.6

  解析

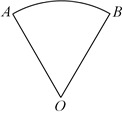• 5．如圖，將扇形AOB圓弧AB拉直后，恰得一邊長為4的等邊三角形，若利用泰勒公式cosx=1-

  x

  2

  2

  !

  +

  x

  4

  4

  !

  -

  x

  6

  6

  !

  +?（n!=n×（n-1）×??×3×2×1）的前三項計算cosx的值，則在扇形AOB中計算

  OA

  ?

  OB

  =（　　）

  A． 26 3

  B． 22 3

  C． 13 3

  D． 11 3
  組卷：36引用：2難度：0.7

  解析

• 6．某群主發了15元的紅包，分成四份，四人領取，均為正整數元，已知其中“運氣王”（“運氣王”是指領到紅包金額最多的人）領到7元，則這四個人不同領取紅包的方法總數為（　　）

  A．84

  B．96

  C．108

  D．120
  組卷：102引用：2難度：0.6

  解析

• 7．已知f（x）是定義在R上的偶函數且f（0）=1，g（x）=f（x-1）是奇函數，則f（1）+f（2）+f（3）+?+f（2021）+f（2022）=（　　）

  A．-2

  B．-1

  C．0

  D．1
  組卷：51引用：2難度：0.6

  解析

四、解答題：本大題共6小題，共70分.解答應寫出文字說明，證明過程或演算步驟.

• 21．已知函數f（x）=

  1

  2

  x²-me^x（m∈R）．
  （1）若f（x）在 R上是單調遞減，求實數m的取值范圍；
  （2）若對任意的x∈（0，+∞），不等式f（x）＞x（

  3

  2

  x-lnx-1）恒成立，求實數m的取值范圍．
  組卷：50引用：2難度：0.4

  解析

• 22．已知函數f（x）=x²-2lnx.
  （1）求函數f（x）的極值；
  （2）設F（x）=f（x）-x²+

  a

  x

  2

  +1（a＜0）有兩個不同的零點x₁，x₂，x₀為其極值點，證明：2F（x₀）＜-

  2

  a

  ＜

  1

  x

  1

  2

  +

  1

  x

  2

  2

  ．
  組卷：59引用：2難度：0.3

  解析