2023年湖北省鄂州市梁子湖區涂家垴中學中考數學模擬試卷
發布：2024/4/20 14:35:0
一、選擇題（本大題共10小題，每小題3分，共計30分）
-
1．實數
的相反數等于（ ）19組卷：89引用：3難度：0.9 -
2．下列圖形中，既是軸對稱圖形又是中心對稱圖形的是（ ）
組卷：204引用：2難度：0.8 -
3．北京冬奧會開幕式的冰雪五環由我國航天科技建造，該五環由21000個LED燈珠組成，夜色中就像閃閃發光的星星，把北京妝扮成了奧運之城．將數據21000用科學記數法表示為（ ）
組卷：280引用：11難度：0.8 -
4．若函數y=ax2-x+1（a為常數）的圖象與x軸只有一個交點，那么a滿足（ ）
組卷：1871引用：22難度：0.7 -
5．“愛勞動，勞動美．”甲、乙兩同學同時從家里出發，分別到距家6km和10km的實踐基地參加勞動．若甲、乙的速度比是3：4，結果甲比乙提前20min到達基地，求甲、乙的速度．設甲的速度為3x km/h,則依題意可列方程為（ ）
組卷：1233引用：25難度：0.7 -
6．一個扇形的弧長是10πcm,其圓心角是150°，此扇形的面積為（ ）
組卷：2017引用：12難度：0.8 -
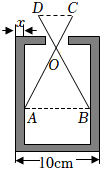7．如圖，某零件的外徑為10cm,用一個交叉卡鉗（兩條尺長AC和BD相等）可測量零件的內孔直徑AB．如果OA：OC=OB：OD=3，且量得CD=3cm,則零件的厚度x為（ ）組卷：2181引用：14難度：0.7 -
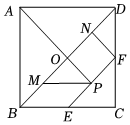8．七巧板是一種古老的中國傳統智力玩具，如圖，在正方形紙板ABCD中，BD為對角線，E，F分別為BC，CD的中點，AP⊥EF分別交BD，EF于O，P兩點，M，N分別為BO，DO的中點，連接MP，NF，沿圖中實線剪開即可得到一副七巧板．則在剪開之前，關于該圖形，下列說法正確的有（ ）
①圖中的三角形都是等腰直角三角形；
②四邊形MPEB是菱形；
③四邊形PFDM的面積占正方形ABCD面積的．14組卷：581引用：4難度：0.4
三、解答題（本大題共8小題，共計72分．解答應寫出必要的文字說明、證明過程或演算步驟）
-
23．問題背景：
一次數學綜合實踐活動課上，小慧發現并證明了關于三角形角平分線的一個結論．如圖1，已知AD是△ABC的角平分線，可證=ABAC．小慧的證明思路是：如圖2，過點C作CE∥AB，交AD的延長線于點E，構造相似三角形來證明BDCD=ABAC．BDCD
嘗試證明：
（1）請參照小慧提供的思路，利用圖2證明：=ABAC；BDCD
應用拓展：
（2）如圖3，在Rt△ABC中，∠BAC=90°，D是邊BC上一點．連接AD，將△ACD沿AD所在直線折疊，點C恰好落在邊AB上的E點處．
①若AC=1，AB=2，求DE的長；
②若BC=m,∠AED=α，求DE的長（用含m,α的式子表示）．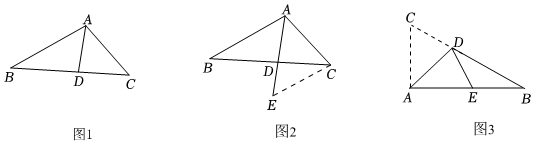
組卷：2537引用：17難度：0.4 -
24．已知拋物線y=ax2+bx-2與x軸交于A（-1，0），B（4，0）兩點，與y軸交于點C．直線l由直線BC平移得到，與y軸交于點E（0，n）．四邊形MNPQ的四個頂點的坐標分別為M（m+1，m+3），N（m+1，m），P（m+5，m），Q（m+5，m+3）．
（1）填空：a=，b=；
（2）若點M在第二象限，直線l與經過點M的雙曲線y=有且只有一個交點，求n2的最大值；kx
（3）當直線l與四邊形MNPQ、拋物線y=ax2+bx-2都有交點時，存在直線l,對于同一條直線l上的交點，直線l與四邊形MNPQ的交點的縱坐標都不大于它與拋物線y=ax2+bx-2的交點的縱坐標．
①當m=-3時，直接寫出n的取值范圍；
②求m的取值范圍．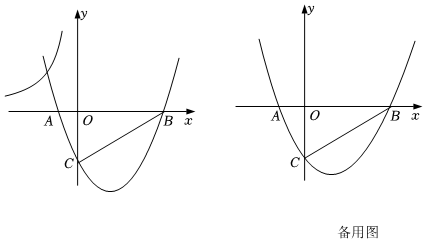
組卷：1450引用：3難度：0.1