2022-2023學(xué)年山東省德州五中七年級(jí)（下）期中數(shù)學(xué)試卷

一、選擇題（每題4分，共48分）

• 1．下列方程中，屬于二元一次方程的是（　　）

  A．x+y-2=0

  B．xy+1=-4

  C．3x2+y=8

  D．x-y-2z=10
  組卷：148引用：3難度：0.8

  解析

• 2．下列各數(shù)：π，0，

  4

  ，

  22

  7

  ，

  2

  .

  5

  ，-3.1415，0.434334…（相鄰的兩個(gè)4之間依次多一個(gè)3），其中無(wú)理數(shù)有（　　）

  A．1個(gè)

  B．2個(gè)

  C．3個(gè)

  D．4個(gè)
  組卷：98引用：3難度：0.6

  解析

• 3．已知

  x = 3

  y = - 2

  是二元一次方程ax+3y=0的解，則點(diǎn)（a,a-3）所在的象限是（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  組卷：572引用：7難度：0.7

  解析

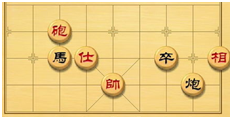• 4．象棋在中國(guó)有著三千多年的歷史，屬于二人對(duì)抗性游戲的一種．由于用具簡(jiǎn)單，趣味性強(qiáng)，成為流行極為廣泛的棋藝活動(dòng)．如圖是一方的棋盤(pán)，如果“帥”的坐標(biāo)是（0，1），“卒”的坐標(biāo)是（2，2），那么“馬”的坐標(biāo)是（　　）

  A．（-2，1）

  B．（2，-2）

  C．（-2，2）

  D．（2，2）
  組卷：523引用：9難度：0.9

  解析

• 5．下列說(shuō)法是真命題的是（　　）

  A．無(wú)理數(shù)都是無(wú)限小數(shù)

  B．過(guò)一點(diǎn)有且只有一條直線與已知直線垂直

  C．方程中含有兩個(gè)未知數(shù)，并且每個(gè)未知數(shù)的次數(shù)都是 1，這樣的方程叫做二元一次方程

  D．直線外一點(diǎn)到這條直線的垂線段叫做點(diǎn)到直線的距離
  組卷：61引用：2難度：0.5

  解析

• 6．若a=

  3

  7

  ，b=

  5

  ，c=2，則a,b,c的大小關(guān)系為（　　）

  A．b＜c＜a

  B．b＜a＜c

  C．a(chǎn)＜c＜b

  D．a(chǎn)＜b＜c
  組卷：2914引用：38難度：0.6

  解析

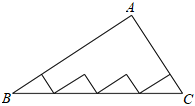• 7．如圖，若四個(gè)完全相同的小直角三角形按如圖方式全部放置在大直角三角形ABC的內(nèi)部，這四個(gè)小三角形的斜邊剛好相接在斜邊BC上，AB+AC=21，BC=15，則這四個(gè)小直角三角形的直角邊之和為（　　）

  A．6

  B．15

  C．21

  D．36
  組卷：318引用：3難度：0.8

  解析

• 8．已知點(diǎn)A（a+1，4），B（3，2a+2），P（b,0），若直線AB∥x軸，點(diǎn)P在x軸的負(fù)半軸上，則點(diǎn)M（b-a,a-2）在（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  組卷：525引用：6難度：0.6

  解析

三、解答題（共7道大題，共78分）

• 24．如圖，在平面直角坐標(biāo)系中，A（a,0），B（b,0），C（-1，2），且|a+2|+（b-3）²=0．
  （1）求a,b的值；
  （2）①在y軸的正半軸上存在一點(diǎn)M，使

  S

  △

  COM

  =

  1

  2

  S

  △

  ABC

  ，求點(diǎn)M的坐標(biāo)；
  ②在坐標(biāo)軸的其他位置是否存在點(diǎn)M，使

  S

  △

  COM

  =

  1

  2

  S

  △

  ABC

  ，仍然成立？若存在請(qǐng)直接寫(xiě)出符合條件的點(diǎn)M的坐標(biāo)．
  組卷：72引用：3難度：0.5

  解析

• 25．【閱讀理解】
  我們經(jīng)常過(guò)某個(gè)點(diǎn)作已知直線的平行線，以便利用平行線的性質(zhì)來(lái)解決問(wèn)題．
  例如：如圖1，AB∥CD，點(diǎn)E、F分別在直線AB、CD上，點(diǎn)P在直線AB、CD之間，設(shè)∠AEP=∠α，∠CFP=∠β，求證：∠P=∠α+∠β．
  證明：如圖2，過(guò)點(diǎn)P作PQ∥AB，
  ∴∠EPQ=∠AEP=∠α，
  ∵PQ∥AB，AB∥CD，
  ∴PQ∥CD，
  ∴∠FPQ=∠CFP=∠β，
  ∴∠EPF=∠EPQ+∠FPQ=∠α+∠β．
  即∠P=∠α+∠β．
  可以運(yùn)用以上結(jié)論解答下列問(wèn)題：
  【類(lèi)比應(yīng)用】
  （1）如圖3，已知AB∥CD，已知∠D=40°，∠GAB=60°，求∠P的度數(shù)；
  （2）如圖4，已知AB∥CD，點(diǎn)E在直線CD上，點(diǎn)P在直線AB上方，連結(jié)PA、PE．設(shè)∠A=∠α、∠CEP=∠β，則∠α、∠β、∠P之間有何數(shù)量關(guān)系？請(qǐng)說(shuō)明理由．
  
  【拓展應(yīng)用】
  （3）如圖5，已知AB∥CD，點(diǎn)E在直線CD上，點(diǎn)P在直線AB上方，連結(jié)PA、PE，∠PED的角平分線與∠PAB的角平分線所在直線交于點(diǎn)Q，求

  1

  2

  ∠

  P

  +

  ∠

  Q

  的度數(shù)．
  組卷：1403引用：6難度：0.4

  解析