2016年第十四屆“走美杯”小學(xué)數(shù)學(xué)競(jìng)賽試卷（三年級(jí)初賽B卷）

一、填空題Ⅰ（每題8分，滿分40分）

• 1．計(jì)算：123456789×8+9=

  ．
  組卷：68引用：1難度：0.9

  解析

• 2．給定一個(gè)除數(shù)（不為0）與被除數(shù)，總可以找到一個(gè)商與一個(gè)余數(shù)．滿足
  被除數(shù)=除數(shù)×商+余數(shù)
  其中，0≤余數(shù)＜除數(shù)．這就是帶余數(shù)的除法，當(dāng)余數(shù)為0時(shí)，也稱除數(shù)整除被除數(shù)，或者稱除數(shù)是被除數(shù)的因數(shù)（被除數(shù)是除數(shù)的倍數(shù)）．
  請(qǐng)寫出所有不超過88并且能夠被6整除的大于1的自然數(shù)

  ．
  組卷：79引用：1難度：0.9

  解析

• 3．只能被1與其自身整除的大于1的自然數(shù)稱為素?cái)?shù)或質(zhì)數(shù)，比如2，3，5，7，11，13等．請(qǐng)?jiān)谝韵聰?shù)表中用圓圈圈出所有的素?cái)?shù)．
  組卷：122引用：1難度：0.9

  解析

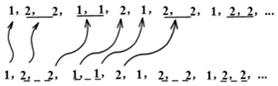• 4．以下由1，2構(gòu)成的無(wú)窮數(shù)列有一個(gè)有趣的特征：從第一項(xiàng)開始，把數(shù)字相同的項(xiàng)合成一個(gè)組，再按照順序?qū)⒚拷M的項(xiàng)數(shù)寫下來(lái)，則這些數(shù)構(gòu)成的無(wú)窮數(shù)列恰好是它自身．這個(gè)數(shù)列被稱為庫(kù)拉庫(kù)斯基數(shù)列．按照這個(gè)特征，繼續(xù)寫出這個(gè)數(shù)列后8項(xiàng)為

  （從第13項(xiàng)到第20項(xiàng)）．
  組卷：72引用：1難度：0.5

  解析

• 5．將自然數(shù)15的0倍，1倍，2倍，3倍，4倍，5倍，…按照順序?qū)懺谙旅?br />0，15，30，45，60，75，…
  這一列數(shù)可以一直寫下去，并且后一個(gè)總比前一個(gè)數(shù)大，任何一個(gè)自然數(shù)要么是這一列數(shù)中的某一個(gè)，要么介于相鄰的兩個(gè)數(shù)之間．我們把這一列數(shù)叫做嚴(yán)格遞增的無(wú)窮數(shù)列，從左至右的每一個(gè)數(shù)分別叫做這個(gè)數(shù)列的第一項(xiàng)，第二項(xiàng)，第三項(xiàng)，…，即第一項(xiàng)是0，第二項(xiàng)是15，第三項(xiàng)是30，…，依此類推．那么，2016介于這個(gè)數(shù)列的第

  項(xiàng)與第

  項(xiàng)之間，這兩項(xiàng)中的較大的項(xiàng)與2016的差是

  ．
  組卷：121引用：1難度：0.7

  解析

三、填空題Ⅲ（每題12分，滿分60分）

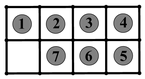• 14．在一個(gè)擺滿棋子的長(zhǎng)方形棋盤中，甲、乙兩人輪流拿取棋子，規(guī)則為：在某行或某列中，取走任意連續(xù)放置的棋子（即不能跨空格拿取），不允許不取，也不能在多行（多列）中拿取．當(dāng)棋盤中所有棋子被取盡時(shí)游戲結(jié)束．取走最后一顆棋子的一方獲勝．面對(duì)如圖所示的棋盤，先手有必勝策略．先手第一步應(yīng)該取走

  （寫出所有的正確方案），才能確保獲勝．
  組卷：141引用：1難度：0.5

  解析

• 15．在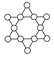的圓圈中填入從1到12的自然數(shù)（每一個(gè)數(shù)用而且只能用一次），使連接在同一直線上的4個(gè)圓圈中的數(shù)字之和都相等，這稱為一個(gè)6階幻星圖，這個(gè)相等的數(shù)稱為6階幻星圖的幻和，那么，6階幻星圖的幻和為

  ，并繼續(xù)完成以下6階幻星圖：
  
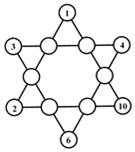  組卷：164引用：1難度：0.3

  解析