2023-2024學年重慶市高二（上）入學數學試卷

一、單項選擇題：本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．

• 1．已知復數z=1+2i（i為虛數單位），則

  z

  的虛部為（　　）

  A．2

  B．-2

  C．2i

  D．-2i
  組卷：59引用：3難度：0.9

  解析

• 2．已知向量

  a

  =（cos120°，sin120°），

  b

  =（1，0），則

  a

  在

  b

  上的投影向量為（　　）

  A．- 3 2 b

  B．- 1 2 b

  C． 1 2 b

  D． 3 2 b
  組卷：92引用：5難度：0.7

  解析

• 3．在△ABC中，

  cos

  A

  =

  3

  5

  ，tanB=2，則tan（A+B）=（　　）

  A．2

  B． 5 3

  C．-2

  D． - 5 3
  組卷：119引用：4難度：0.7

  解析

• 4．已知α，β是空間中兩個不同的平面，m,n是空間中兩條不同的直線，則（　　）

  A．若m∥α，n∥α，則m∥n	B．若m∥α，m∥β，則α∥β
  C．若α⊥β，m?α，則m⊥β	D．若m⊥α，n⊥β，m⊥n,則α⊥β
  組卷：61引用：3難度：0.7

  解析

• 5．已知函數

  y

  =

  1

  +

  cos

  2

  ωx

  2

  （

  ω

  ＞

  0

  ）

  在

  [

  -

  π

  4

  ，

  π

  6

  ]

  上的最小值為

  1

  4

  ，則ω的值為（　　）

  A．1

  B． 2 3

  C． 4 3

  D．2
  組卷：60引用：2難度：0.7

  解析

• 6．某圓臺的側面展開是一個半圓環（如圖所示），且其中內、外半圓弧所在圓的半徑分別為2和6，則該圓臺的體積為（　　）

  A． 14 3 3 π

  B． 26 3 3 π

  C． 26 3 π

  D． 52 3 π
  組卷：81引用：4難度：0.7

  解析

• 7．如圖，在四棱錐P-ABCD中，PA⊥平面ABCD，正方形ABCD的邊長為2，PA=4，E為側棱PC的中點，則異面直線BE與PA所成角的正切值為（　　）

  A． 2 4

  B． 2

  C．1

  D． 2 2
  組卷：444引用：7難度：0.7

  解析

四、解答題：本大題共6個大題，共70分．解答應寫出文字說明、證明過程或演算步驟．

• 21．函數f（x）=Msin（ωx+φ）（M＞0，ω＞0，|φ|＜

  π

  2

  ）的部分圖象如圖所示．已知A（-

  1

  6

  ，0），B（

  1

  3

  ，M），C（x₀，-M），AB⊥AC．
  （1）求x₀和f（x）的解析式；
  （2）將f（x）的圖象向右平移

  1

  3

  個單位長度，再將得到的圖象上各點的橫坐標縮短為原來的

  1

  2

  ，縱坐標不變，得到函數g（x）的圖象，求g（x）在[0，

  1

  2

  ]上的值域．
  組卷：155引用：4難度：0.5

  解析

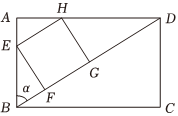• 22．中國剪紙是一種民間藝術．具有廣泛的群眾基礎，交融于各族人民的社會生活，現有一張矩形卡片ABCD，對角線長為t（t為常數），從△ABD中裁出一個內接正方形紙片EFGH，使得點E，H分別AB，AD上，設

  ∠

  DBA

  =

  α

  （

  0

  ＜

  α

  ＜

  π

  2

  ）

  ，矩形紙片ABCD的面積為S₁，正方形紙片EFGH的面積為S₂．
  （1）當

  α

  =

  π

  3

  時，求正方形紙片EFGH的邊長（結果用t表示）；
  （2）當α變化時，求

  S

  2

  S

  1

  的最大值及對應的α值．
  組卷：46引用：3難度：0.5

  解析