2023-2024學年上海市奉賢中學高二（上）月考數學試卷（10月份）

一、填空題（本大題共有12小題，滿分54分，第1-6題每題4分，第7-12題每題5分）

• 1．已知點A（0，0），B（2，3），則直線AB的傾斜角α=

  ．
  組卷：26引用：2難度：0.8

  解析

• 2．已知向量

  a

  =

  （

  -

  3

  ，

  2

  ，

  4

  ）

  ，

  b

  =

  （

  1

  ，-

  2

  ，

  2

  ）

  ，則

  |

  a

  -

  b

  |

  =

  ．
  組卷：33引用：2難度：0.5

  解析

• 3．過點（-2，3）且與直線2x+y+1=0垂直的直線l的方程是

  ．
  組卷：140引用：6難度：0.8

  解析

• 4．已知向量

  a

  =

  （

  2

  ，

  1

  ，

  3

  ）

  ，

  b

  =

  （

  1

  ，

  1

  ，-

  1

  ）

  ，

  c

  =

  （

  4

  ，

  3

  ，

  m

  ）

  ，若

  a

  ，

  b

  ，

  c

  共面，則m=

  ．
  組卷：60引用：3難度：0.5

  解析

• 5．若直線l₁：3kx-（k+2）y+6=0和直線l₂：kx+（2k-3）y+2=0斜率互為相反數，則k=

  ．
  組卷：51引用：1難度：0.8

  解析

• 6．點

  A

  （

  3

  2

  ，

  2

  ）

  關于直線

  x

  +

  y

  +

  1

  3

  =

  0

  的對稱點為

  ．
  組卷：97引用：2難度：0.6

  解析

• 7．已知平面α的一個法向量為

  n

  =

  （

  1

  ，-

  1

  ，

  1

  ）

  ，直線l的一個方向向量為

  m

  =

  （

  2

  ，

  2

  ，

  0

  ）

  ，則直線l與平面α的位置關系是

  ．
  組卷：29引用：1難度：0.8

  解析

三、解答題（本大題共5題，滿分78分）

• 20．已知直線l：ax-y+2-a=0恒過點P，且與x軸，y軸分別交于A，B兩點，O為坐標原點．
  （1）求點P的坐標；
  （2）當點O到直線l的距離最大時，求直線l的方程；
  （3）當|PA|?|PB|取得最小值時，求△AOB的面積．
  組卷：396引用：9難度：0.7

  解析

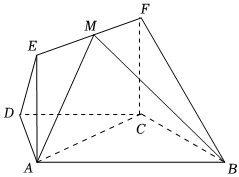• 21．如圖，在梯形ABCD中，AB∥CD，AD=DC=CB=1，∠ABC=60°，四邊形ACFE為矩形，平面ACFE⊥平面ABCD，CF=1．
  （1）求證：BC⊥平面ACFE；
  （2）求平面ABF與平面BCF所成角的大小；
  （3）若點M在線段EF上運動，設平面MAB與平面FCB所成二面角的平面角為θ（θ≤90°），試求cosθ的范圍．
  組卷：50引用：1難度：0.4

  解析