2022-2023學年福建省泉州科技中學高一(下)期中數學試卷
發布:2024/5/6 8:0:9
一、單選題(本大題共8小題,共40分)
-
1.已知
,則cosθ=23=( )sin(2θ+π2)A. -19B. 19C. -89D. 89組卷:459引用:2難度:0.8 -
2.已知向量
=(2,4),a=(-1,1),則2b-a=( )bA.(5,7) B.(5,9) C.(3,7) D.(3,9) 組卷:3973引用:69難度:0.9 -
3.下列等式不成立的是( )
A. cos215°-sin215°=32B. sinπ8cosπ8=24C. 12sin40°+32cos40°=sin70°D. tan15°=2-3組卷:63引用:1難度:0.6 -
4.為了得到函數
的圖象,只要把y=cos2x的圖象上所有點( )y=cos(2x+π3)A.向左平移 個單位長度π6B.向右平移 個單位長度π6C.向左平移 個單位長度π3D.向右平移 個單位長度π3組卷:48引用:2難度:0.7 -
5.已知單位向量
,a滿足b,則向量|2a-b|=23a?b,a的夾角為( )bA. 2π3B. π2C. π3D. π4組卷:138引用:3難度:0.8 -
6.已知cos(α-β)=
,cos2α=55,α∈(0,1010),β∈(0,π),且α<β,則α+β=( )π2A. π4B. 3π4C. 5π6D. 5π4組卷:192引用:2難度:0.8 -
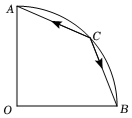 7.如圖,已知兩個模都為10的向量,它們的夾角為OA,OB,點C在以O為圓心,10為半徑的π2上運動,則?AB的最小值為( )CA?CB
7.如圖,已知兩個模都為10的向量,它們的夾角為OA,OB,點C在以O為圓心,10為半徑的π2上運動,則?AB的最小值為( )CA?CBA. 100-1002B.-100 C. 1002-100D. -1002組卷:130引用:4難度:0.6
四、解答題(本大題共6小題,共70分。解答應寫出文字說明,證明過程或演算步驟)
-
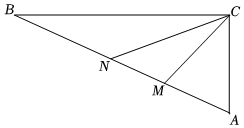 21.為響應國家“鄉村振興”號召,農民王大伯擬將自家一塊直角三角形地按如圖規劃成3個功能區:
21.為響應國家“鄉村振興”號召,農民王大伯擬將自家一塊直角三角形地按如圖規劃成3個功能區:
△BNC區域為荔枝林和放養走地雞,△CMA區域規劃為“民宿”供游客住宿及餐飲,△MNC區域規劃為小型魚塘養魚供休閑垂釣.為安全起見,在魚塘△MNC周圍筑起護欄.已知AC=40m,,AC⊥BC,∠MCN=30°.BC=403m
(1)若AM=20m時,求護欄的長度(△MNC的周長);
(2)當∠ACM為何值時,魚塘△MNC的面積最小,最小面積是多少?組卷:161引用:9難度:0.6 -
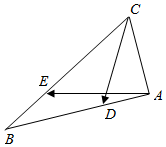 22.如圖,在△ABC中,已知CA=1,CB=2,∠ACB=60°.
22.如圖,在△ABC中,已知CA=1,CB=2,∠ACB=60°.
(1)求||;AB
(2)已知點D是AB上一點,滿足=λAD,點E是邊CB上一點,滿足AB=λBE.BC
①當λ=時,求12?AE;CD
②是否存在非零實數λ,使得⊥AE?若存在,求出λ的值;若不存在,請說明理由.CD組卷:565引用:20難度:0.1


