2023-2024學年北京市中國人民大學附中高二（上）期中數學試卷
發布：2024/10/18 19:0:2
一、選擇題（本大題共10小題，每小題4分，共40分。在每小題給出的四個選項中，只有一項是符合題目要求的，請將正確答案填涂在答題紙上的相應位置.）
-
1．已知平面α∥平面β，直線a?α，直線b?β，則a與b的位置關系是（ ）
組卷：146引用：2難度：0.4 -
2．空間中點A的坐標是（3，-1，0），若向量
，則點B的坐標是（ ）AB=（2，5，-3）組卷：137引用：1難度：0.5 -
3．一個水平放置的平面圖形△OAB用斜二測畫法作出的直觀圖是如圖所示的等腰直角△O′A′B′，其中A′B′=，則平面圖形△OAB的面積為（ ）10組卷：523引用：5難度：0.8 -
4．已知cos＜
，a＞=-b，則下列說法錯誤的是（ ）13組卷：114引用：3難度：0.6 -
5．一個三棱錐的各棱長均相等，其內部有一個內切球，即球與三棱錐的各面均相切（球在三棱錐的內部，且球與三棱錐的各面只有一個交點），過一條側棱和對邊的中點作三棱錐的截面，所得截面圖形是（ ）
組卷：319引用：8難度：0.7 -
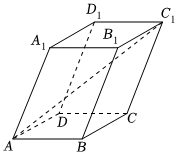6．如圖，平行六面體ABCD-A1B1C1D1的底面ABCD是矩形，其中AB=2，AD=4，AA1=3，且∠A1AD=∠A1AB=60°，則線段AC1的長為（ ）組卷：211引用：9難度：0.5 -
7．如圖，已知大小為60°的二面角α-l-β棱上有兩點A，B，AC?α，AC⊥l,BD?β，BD⊥l,若AC=3，BD=3，CD=7，則AB的長為（ ）組卷：305引用：10難度：0.5 -
8．魯班鎖是中國傳統的智力玩具，起源于中國古代建筑中首創的榫卯結構，它的外觀是如圖所示的十字立方體，其上下、左右、前后完全對稱，六根完全一樣的正四棱柱體分成三組，經90°榫卯起來．若正四棱柱的高為6，底面正方形的邊長為1，現將該魯班鎖放進一個球形容器（容器壁的厚度忽略不計），則該球形容器表面積的最小值為（ ）組卷：348引用：10難度：0.7
五、填空題（共3小題，每小題5分，共15分，把答案填在答題紙上的相應位置.）
-
25．點O是正四面體A1A2A3A4的外接球球心，|OAi|=1（i=1，2，3，4）．若
，其中0≤λ1≤1（i=1，2，3，4），則動點P掃過的區域的體積為 ．OP=λ1OA1+λ2OA2+λOA3+λOA4組卷：32引用：1難度：0.5
六、解答題（本小題15分，解答應寫出文字說明過程或演算步驟，請將答案寫在答題紙上的相應位置.）
-
26．已知自然數集A={1，2，3，?，n}（n∈N*），非空集合
．若集合E滿足：對任意a∈A，存在ei，ej∈E（1≤i≤j≤m），使得a=xei+yej，x,y∈{-1，0，1}，稱集合E為集合A的一組m元基底．E={e1，e2，?，em}?A（m∈N*）
（1）分別判斷下列集合E是否為集合A的一組二元基底，并說明理由：
①E={1，2}，A={1，2，3，4，5}；
②E={2，3}，A={1，2，3，4，5，6}．
（2）若集合E是集合A的一組m元基底，證明：n≤m（m+1）；
（3）若集合E為集合A={1，2，3，?，19}的一組m元基底，求m的最小值．組卷：50引用：2難度：0.5